2024年度 京大入試(理系数学)レビュー:根本的な理解と、典型的な手法を柔軟に応用させる力が差を生むセット
こんにちは。品川区にある大学受験のための少人数制の学習塾「Dear Hope」副塾長の伊藤です。
今日は,先日実施された国立大の入試から,京都大学(理系)の数学について所感など記していきたいと思います。
今年は,平易な問題から難易度の高い問題までバランス良く配置されたセットだったと思います。解いていて面白いなと思いました。今年のセットは次の通りです。
(第1問) 立方体の各面を異なるn色で塗り分けるときに,辺を共有するどの二つの面にも異なる色が塗られる確率を求める問題。
立方体の塗り分けというと,一面を固定した上で側面を円順列で塗り分けるという解法が有名です。しかし今回は場合の数ではなく「確率」の出題です。この違いをきちんと理解できていた人にとっては取り組みやすい問題だったでしょう。
(第2問) 複素数平面上で定義された二つの図形それぞれの上を動く動点の中点が動く領域を求める問題。
いわゆる予選決勝法(2つの動点のうち一方を固定して他方を動かし,次に固定していた動点を動かす,という2段階の手続きで像を求める手法)の問題で,今年のセットでは落とせない一問。
(第3問) 座標空間内に定義された2つの直線がねじれの位置にあるための条件を求める問題。
題意を満たす変数(x, y)の補集合を考えることに気づけば,あとはベクトルの簡単な計算手続きで答えが得られる問題。これもぜひ完答したい一問。
(第4問) 項の偶奇に応じて別々の漸化式で定められた数列の初項から第3項まで((2)では第10項まで)のすべての項が奇数になるように初項を定める問題。
表向きは数列の問題ですが,どのように論証するかがポイント。答えだけあっていても論証が足りない場合はほぼ得点できないと思われる問題です。あとで詳しく見ていきたいと思います。
(第5問) 座標平面において,連立不等式で定義された領域の面積とその極限値を求める問題。
本問は,計算力を試す問題でした。有名なタイプの問題ではありますが,一度解いたことが無いと手間取ったでしょう。また,(2)の極限値を求める計算は難易度高めです。
(第6問) 与えられた数列{ak}について,「n桁となる項の個数と,n桁であり最高位の数が1でもある項の個数との比」の極限値を求める問題
ガウス記号を用いるなどして比率を求め,ハサミウチの原理により極限値を求めていきます。易しくはありませんが,典型的です。
独断と偏見による難易度としては,
(易)2<3≦1<6≦4<5(難)
だと思います。全体として難易度は高めて,実力の差が明確に得点に表れたのではないかと想像しています。以下,いくつかの問題を引用しつつ,コメントしたいと思います。
〔第1問〕

(出典:2024年度 京都大学入試問題 数学(理系)第1問)
まず注意すべきは,本問は場合の数の問題ではなく,「確率」の問題であるということです。したがって,立方体の各面に1~6の番号を振るなどして各面を区別して考えていくのが良いでしょう。
立方体を塗り分ける方法(場合の数)であれば,立方体が回転することで一致してしまう塗り方を重複してカウントしないように注意しなければなりません。このため,先に述べたように,立方体の一つの面を特定の色に固定してしまって,次に底面の色の塗り方,そして側面の塗り方(これは円順列になります)を考えていきます。
しかし本問でこのような考え方を採用すると,誤答の危険性があるので注意が必要です。そのあたりのことを正確に理解しているかを問うています。
理解されている方には釈迦に説法ですが,念のため「nCr」の意味を確認しておきます。
授業で「nCr」とはどのような場合の数を表しますか?と尋ねると,たいてい,「n個のものからr個を選ぶ場合の数です。」というような答えが返ってきます。大体正しいのですが,正確ではありません。正確には「『相異なる』n個のものからr個を選ぶ場合の数」ですね。
このことを納得してもらった上で,さらに次の問いを続けます。
(問題)赤玉4個,白玉3個が袋に入っている。この中から無作為に3個の玉を取り出すとき,赤玉が2個,白玉が1個取り出される確率を求めよ。
(答え)
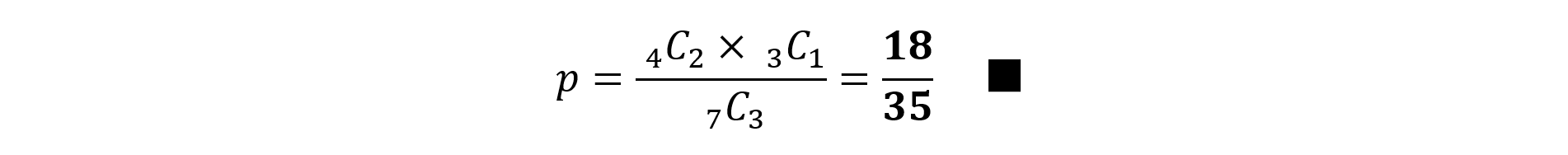
さて,この答え自体は正しいのですが,この計算プロセスを正確に理解していない(忘れてしまっている?)生徒さんは,実は少なくありません。先ほどの話を踏まえると,分母の「7C3」は,「『相異なる』7個の玉から3個を選ぶ場合の数」です。本問では,7個の玉のうち4個の赤玉は「相異なって」いません。白玉についても同様です。なのに,なぜ上のような解き方で良いのでしょうか。
その理由は,計算を実行する前に,作為的に赤玉と白玉にそれぞれ1~4,1~3の番号を振るなどして,7個の玉を「相異ならせている」からでしたよね。この工夫により,「7C3」や「4C2」という組み合わせの式で簡単に処理できるわけです。
したがって,分母の「7C3」とは,「(互いに区別の無い)赤玉4個と(互いに区別の無い)白玉3個の計7個の玉から3つの玉を取り出す場合の数」ではないということです!
以上を踏まえると,本問においても,まず立方体の各面に番号を振るなどして区別すると簡単に処理できそうだな,と想像できます。では実際に,(1)のp4を求めてみたいと思います。
(全事象)
一つの面の塗り方は4通りある。いま,各面が区別されているから,全体では46通り。
(4色で塗り分ける場合の数)
4色のうち2色はそれぞれ互いに向かい合う2面に塗られる。その2色の決め方は4C2=6通りであり,塗られる面(合計4面)の決め方は3P2=6通り。それぞれの決め方に対し,残り2色の塗り方が2!通り。以上から,6×6×2!=72通り。
(3色で塗り分ける場合の数)
4色から3色を選ぶ方法が4C3=4通り。各色はそれぞれ互いに向かい合う2面に塗られる。その塗り方(面の決め方)は3!通り。以上から,4×3!=24通り。
これらは互いに排反だから,
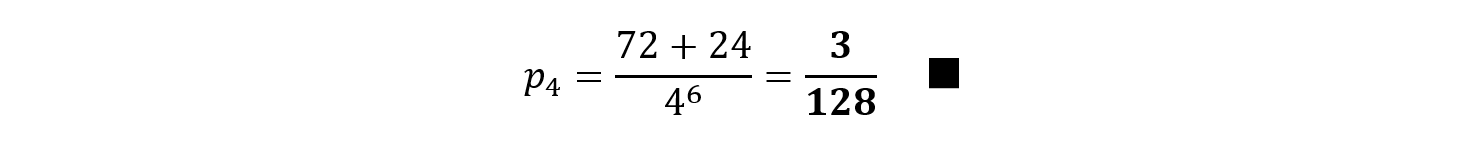
となります。なお,(2)も同様であり,極限値の計算は平易ですので,ここでは省略します。
(第3問)

(出典:2024年度 京都大学入試問題 数学(理系)第3問)
本問は,京都大で頻出の図形問題です。「2直線がねじれの位置にある」ということですがこれは,「2直線が平行でなく,かつ互いに交わらない」ことを言います。これは中学1年生の空間図形で学習する内容です。したがって,この条件を否定すると,ド・モルガン則から,
「2直線が平行であるか,または互いに交わる」(4点Q,Y,P,Xが同一平面上にある)
になります。このようなx, yの条件を求めて否定すれば,題意の必要十分条件が得られます。
「平行」や「交わる」については,ベクトルでさんざんやらされた処理だと思いますので,ここでは省略します。
(第4問)

漸化式にからめた論証問題です。例えば,初項から奇数が連続する条件を次のように考えてみてはいかがでしょうか。
第n項anが奇数である条件は,
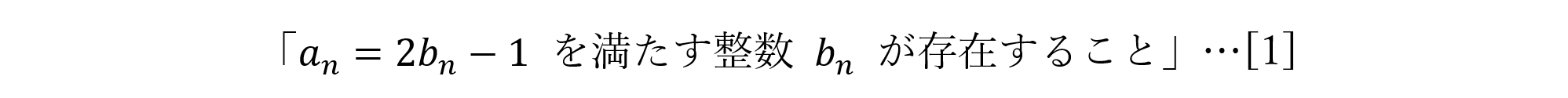
を得ます。同様に,an+1 が奇数である条件は,
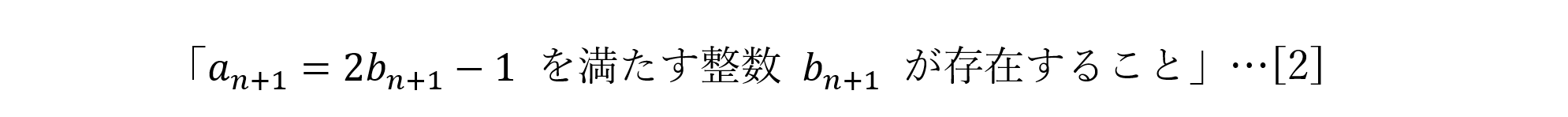
ゆえに,an,an+1がともに奇数となる条件は,[1]かつ[2]が真である条件,すなわち,与えられた漸化式を用いて,
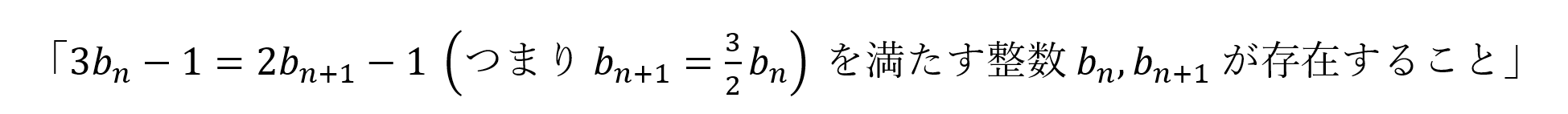
以上から,帰納的に,
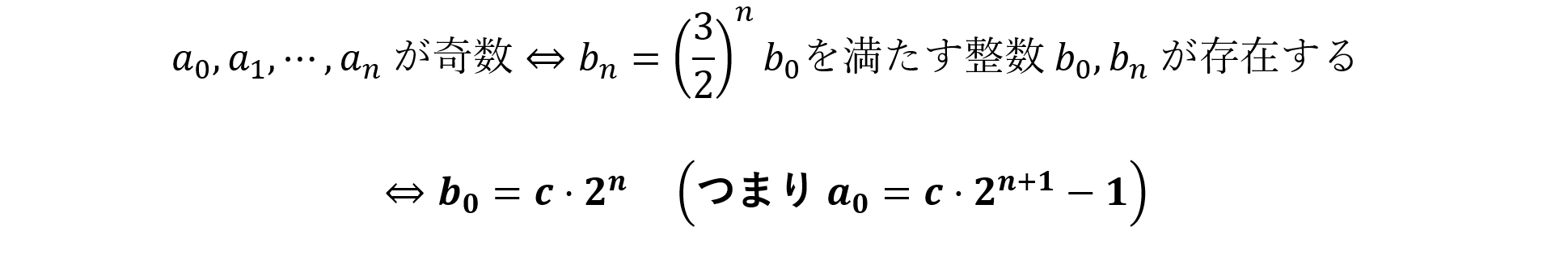
となります。この結果から,(1)においては,
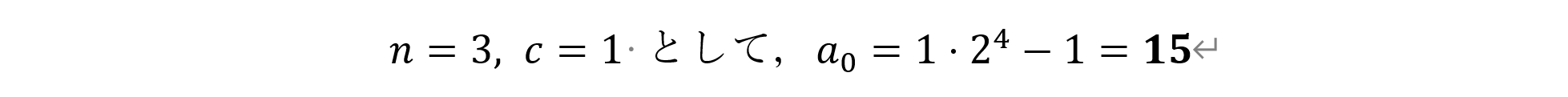
(2)においては,
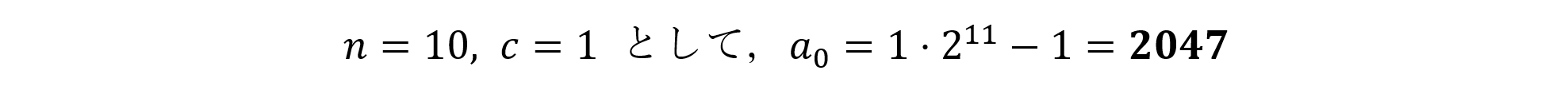
を得ます。
(第5問)

(出典:2024年度 京都大学入試問題 数学(理系)第5問)
本問は,合否を分けた1題ではないかと思いますので,詳しく見ていきたいと思います。
まず,与えられた4つの不等式が表す領域を示します。次の図の水色の部分です。
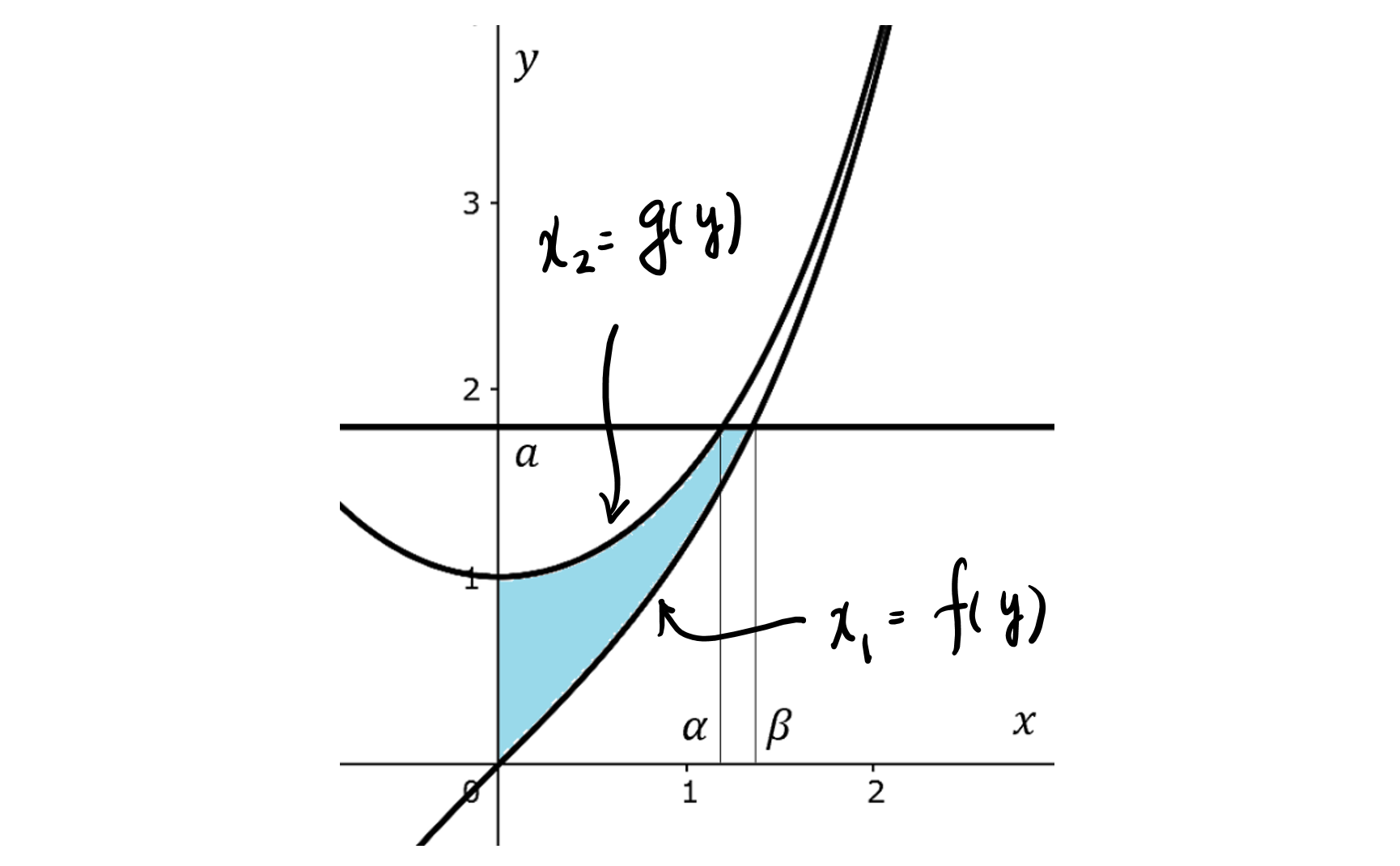
図中のαは,
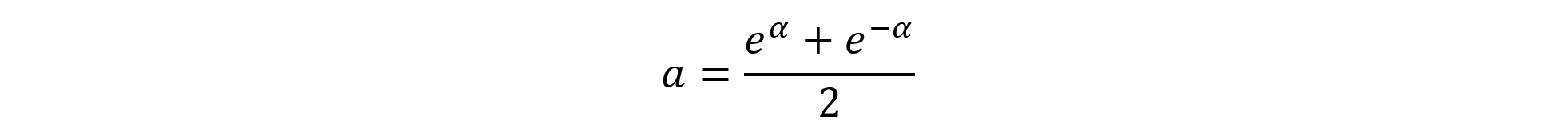
を満たす正の実数だから,eα=A(>0)とおくと,
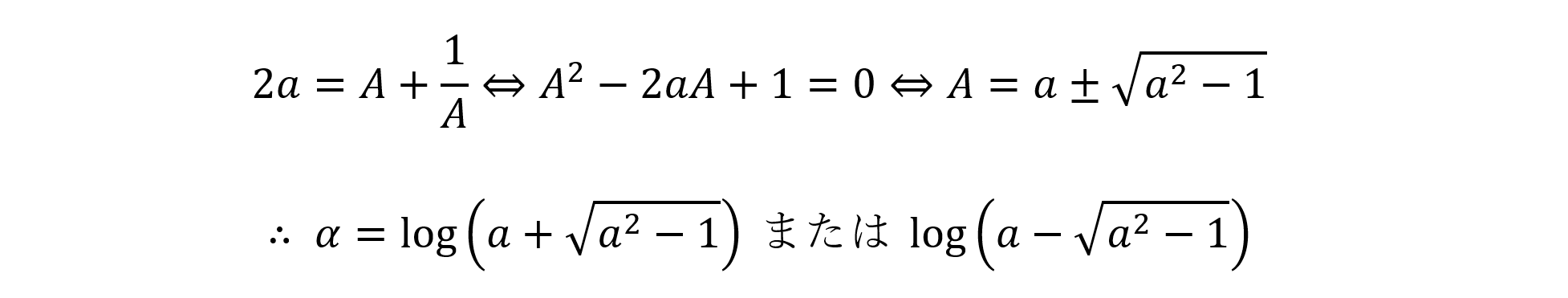
いま,α>0だから,真数は1より大。ゆえに
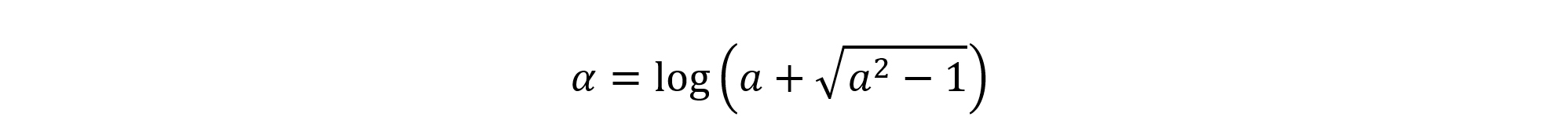
なぜなら,
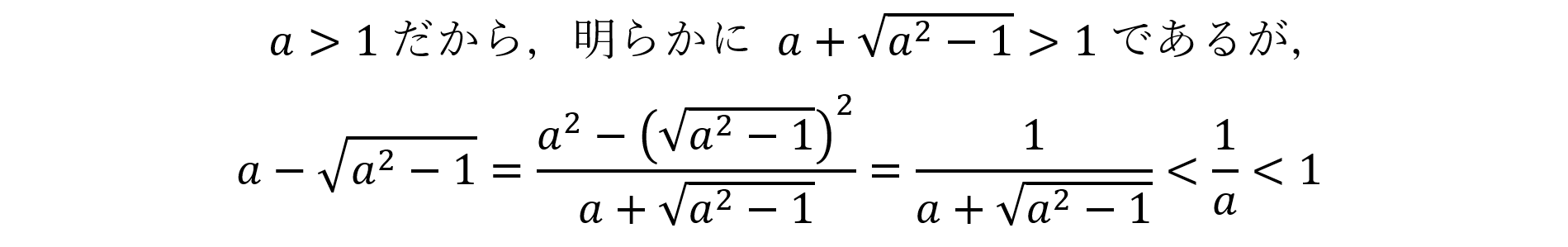
だからです。同様に,
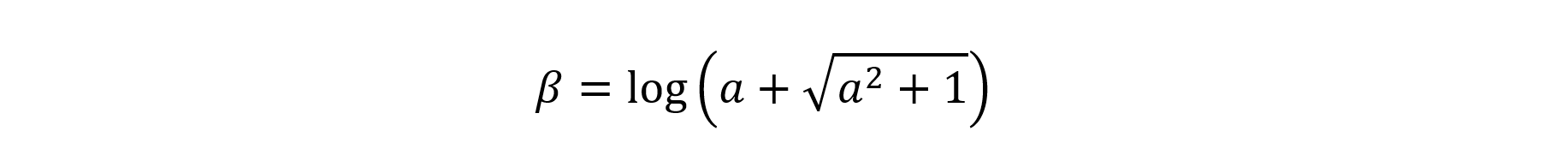
一応このようにしてα,βを求めることができますが,計算を進める上では,
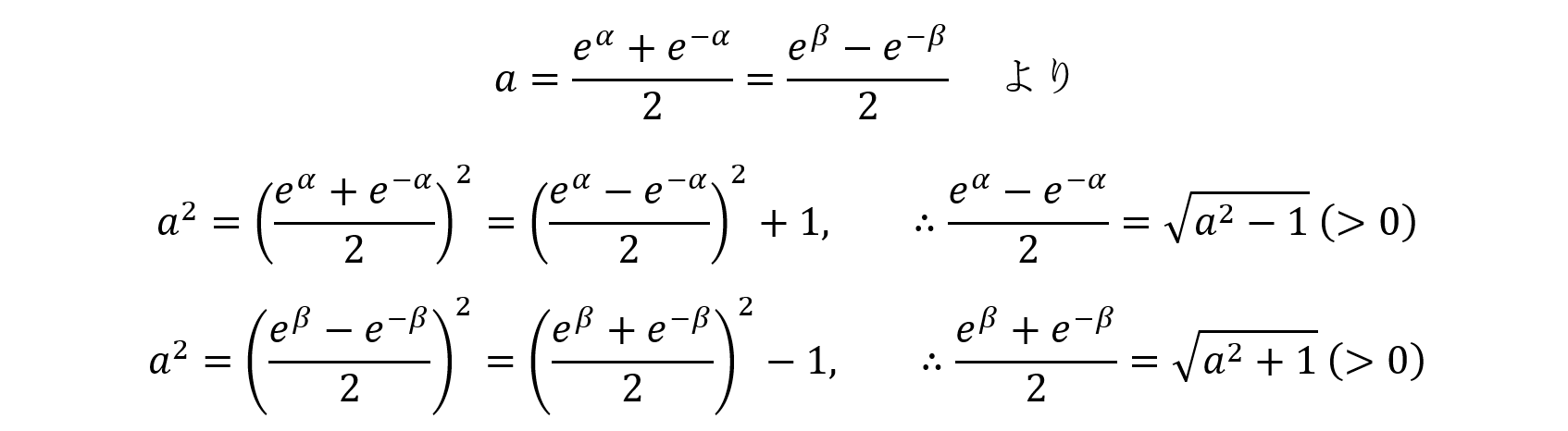
さて,面積Saを求めていきましょう。ここからは基本通りです。
領域の右側の境界および左側の境界を規定しているグラフをそれぞれ x1=f(y), x2=g(y) と表すと,
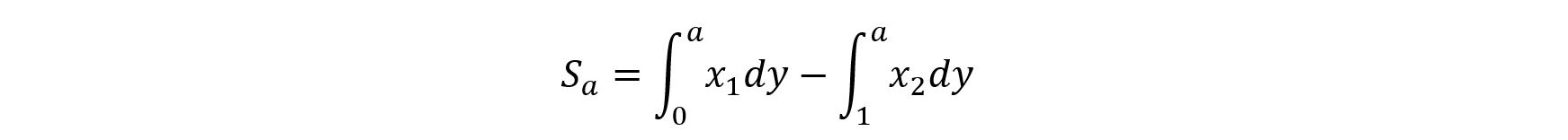
これらの積分変数をxに変換し,部分積分法を利用して,
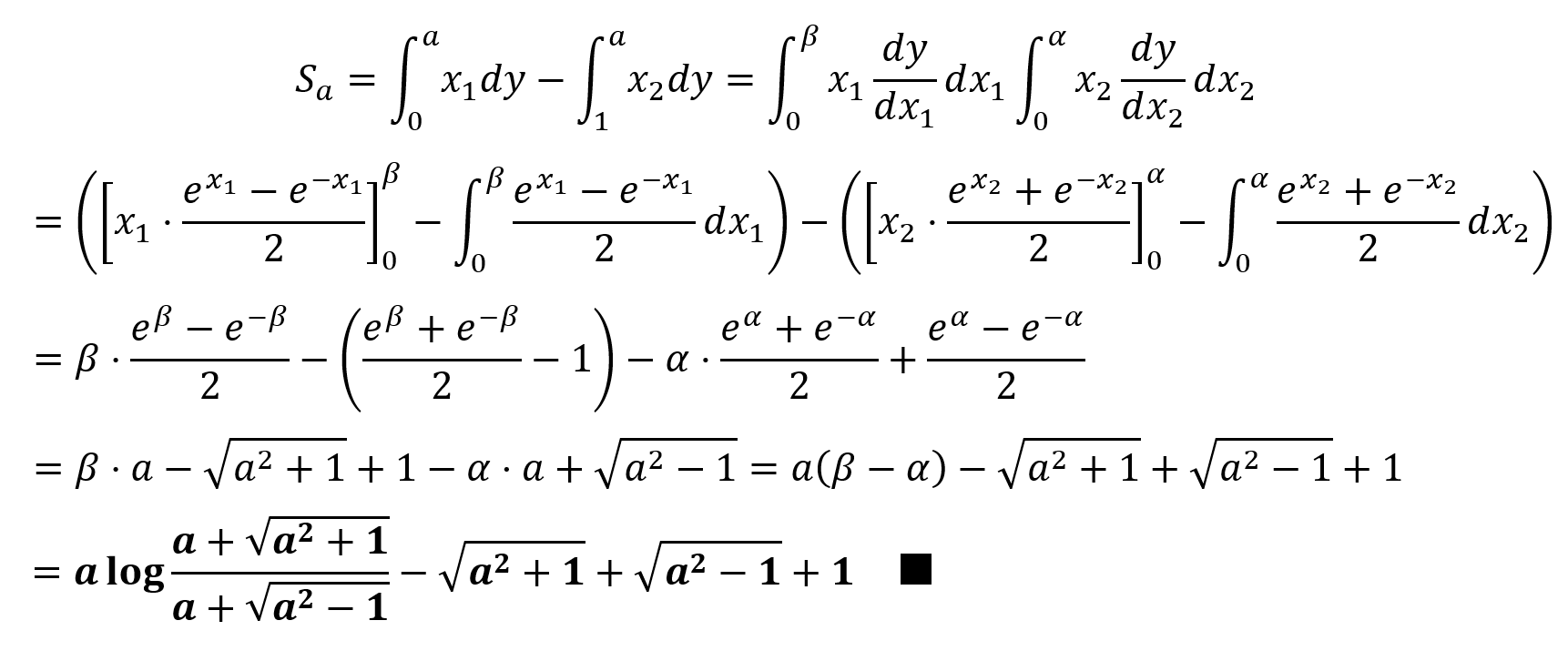
次に(2)です。ここが少し難しかったと思います。上式の第2項と第3項は,
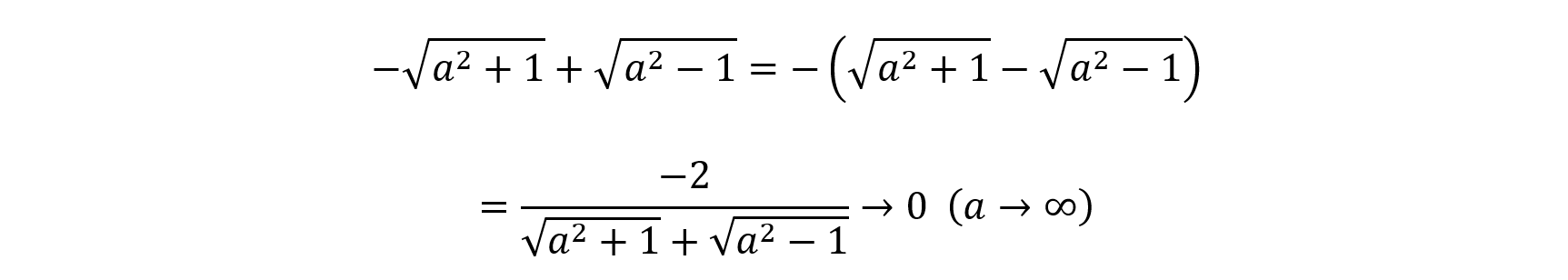
です。したがって,問題となるのは,第1項の
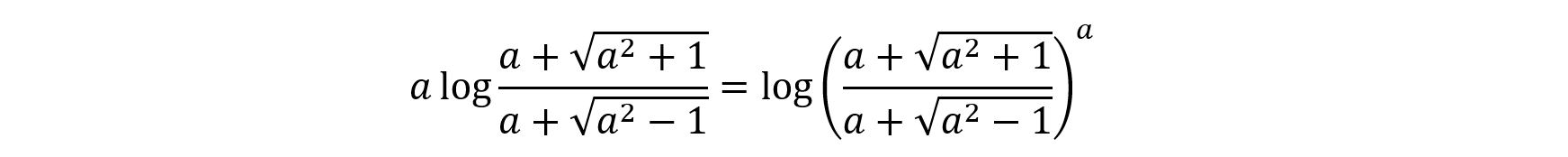
の部分です。
この真数を自然対数の底eの定義
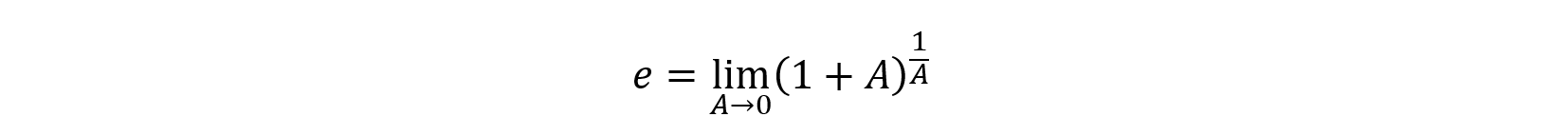
に基づいて処理できないか考えてみましょう。真数は,
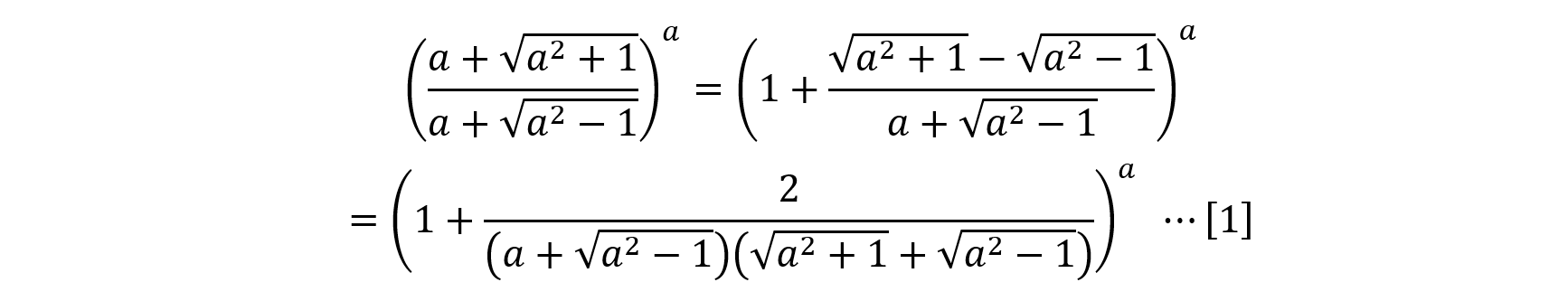
ここで,
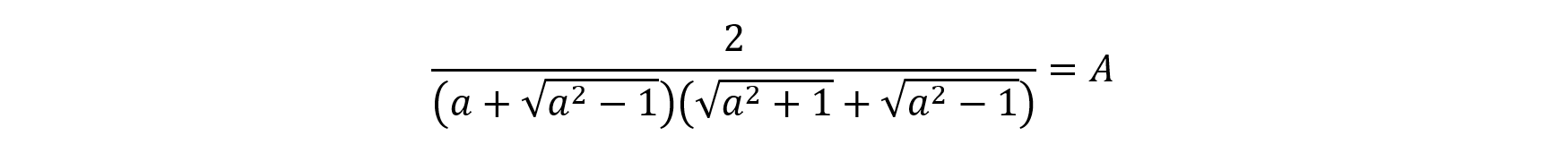
と置換すると,
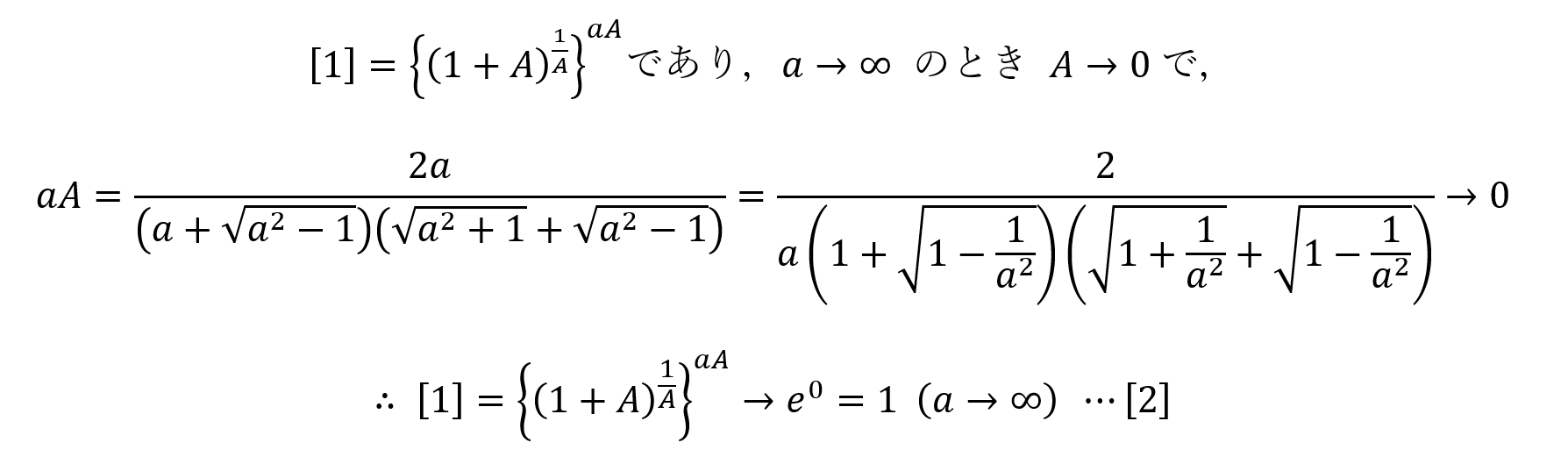
となることが分かりました。
以上を総合すると,結局,
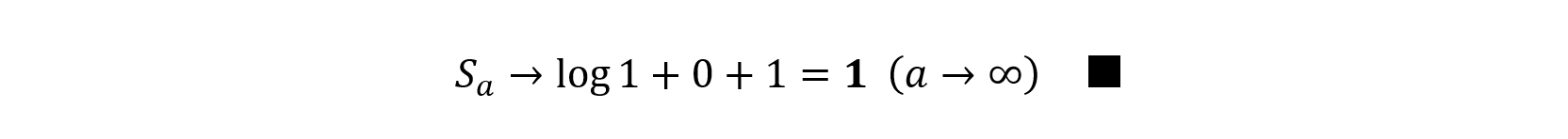
あるいは別解として,a>1だから,上で定義したAについて,
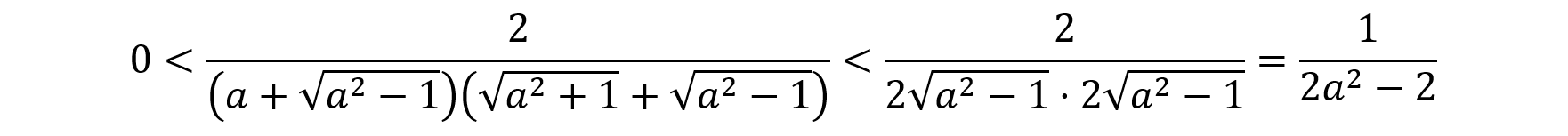
が成り立つため,[1]式を次のように評価することができます。
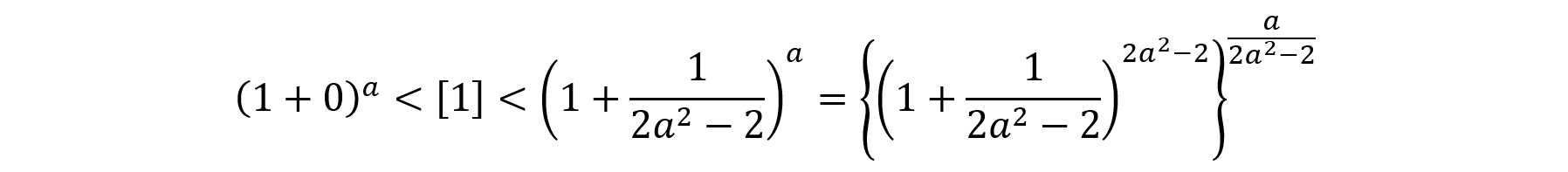
a→∞のとき,右辺も左辺も1(=e0)に収束するから,[1]→1が得られ,[2]の結果と一致しました。
さらに,t=1/aと置換して,微分法の定義に持ち込む方法も考えられます。
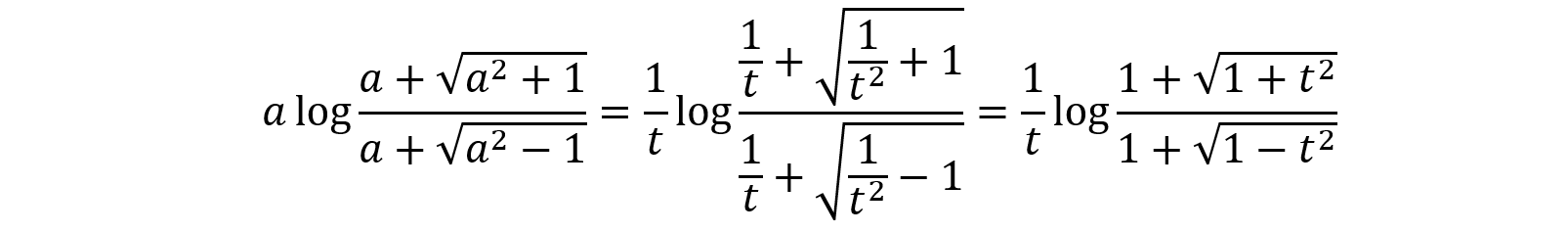
ここで,
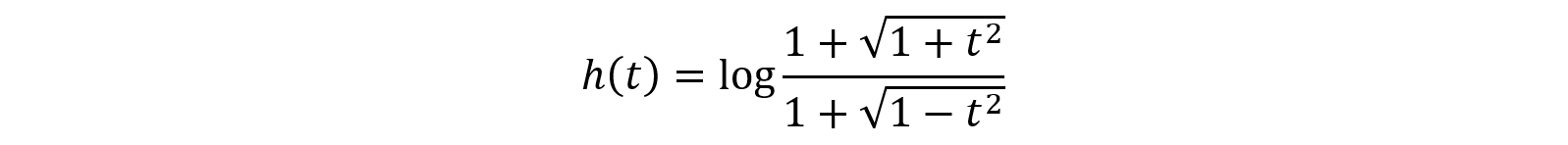
とおくと,h(0)=0だから,微分法の定義から,
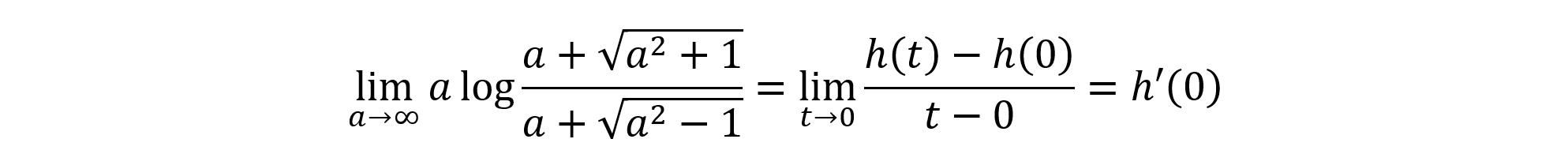
を得ます。あとはh(t)を微分してh’(0)の値を求めればOKです。
最後に,第6問もチェックしておきます。
(第6問)

(出典:2024年度 京都大学入試問題 数学(理系)第6問)
本問は,内容としては典型的で,ハサミウチの原理に持ち込むタイプの問題です。素直に,Nn, Lnを求めてみましょう。
akの整数部分がn桁だから,
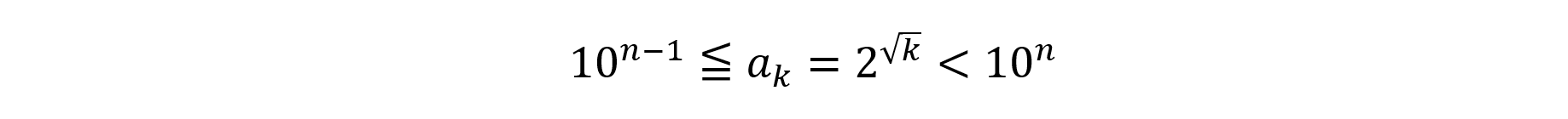
が成立します。各辺の常用対数をとると,
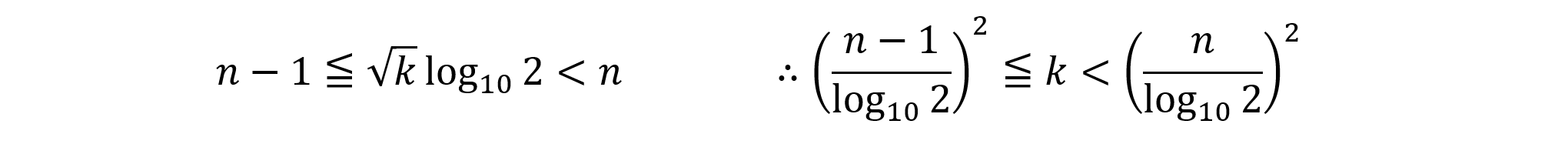
これを満たす自然数kの個数がNnです。
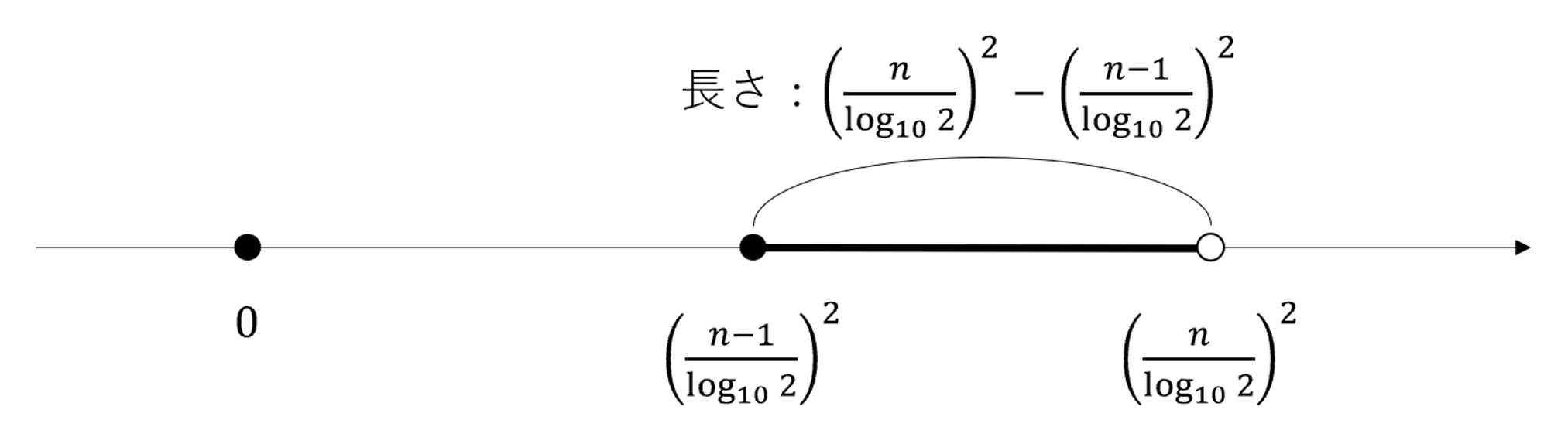
これは上のように数直線で考えるとわかりやすいでしょう。
一般に,数直線上で長さがLの区間(左端を含み,右端を除く)に含まれる整数は,
[L]-1個以上,[L]+1個以下
です。なお,[ ]はガウス記号を表します。したがって,
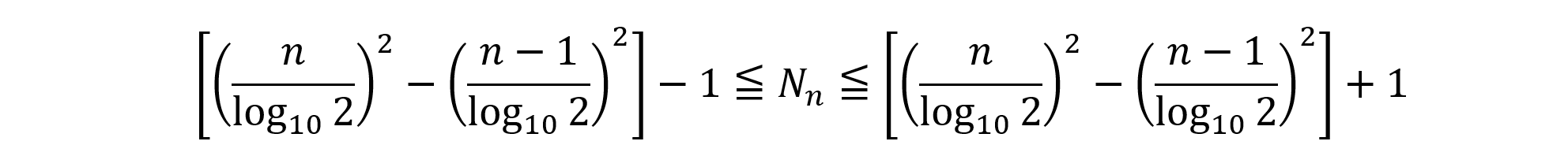
続いて,ガウス記号に関して一般に成立する不等式 x-1<[x]≦x を用いて,ガウス記号を外すと,
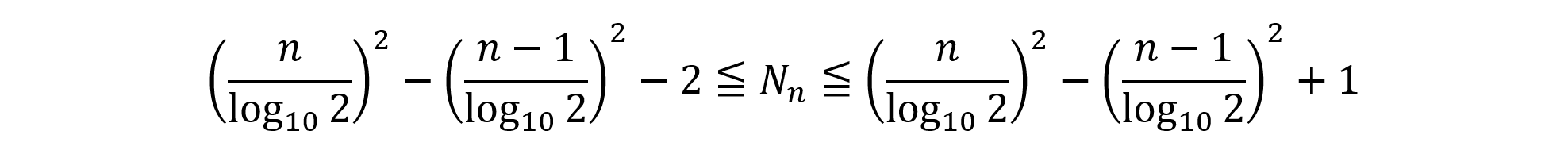
となります。次に,Lnについても同様に求めていきます。
akの整数部分がn桁であり,かつ最高位の数字が1だから,
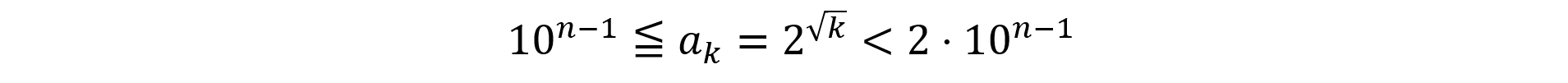
を満たすような自然数kの個数が,Lnです。したがって,
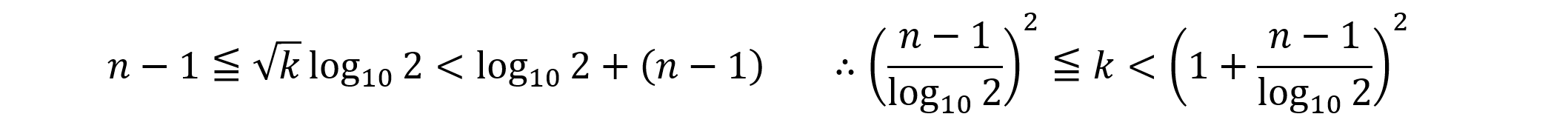
これより,次に不等式を得ます。
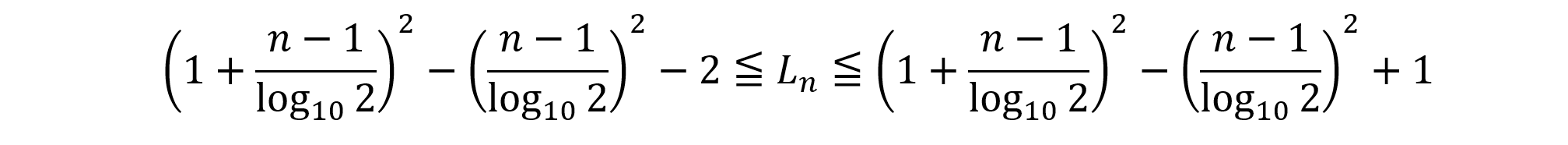
簡単のため,log102=aとおきかえて比をとると(このような置き換えは,式を見やすくして計算の見通しを立てやすくするうえで案外大切な操作です。)
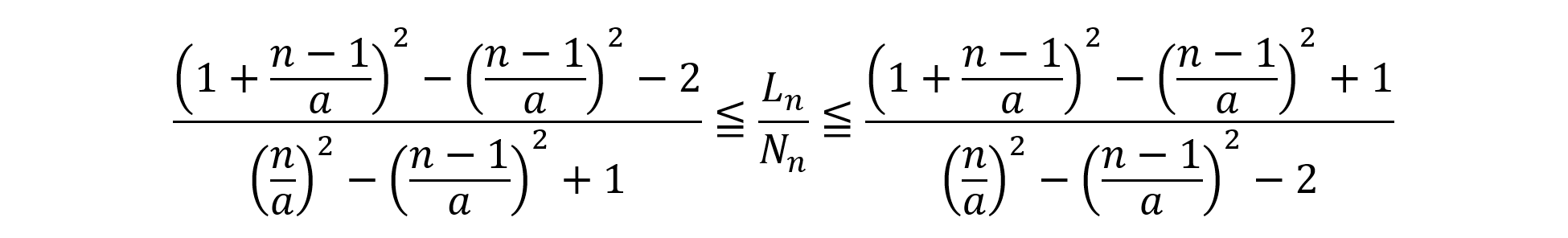
と評価することができます。
右辺と左辺を整理したのち,nを∞に飛ばせばOKです(答えは,log102)。
まとめ
以上のように,今年の京都大(理系)のセットは,全体として難易度が高めで,数学の実力をしっかりと養ってきた受験生とそうでない受験生とで,大きく差が開いたのではないかと思います。
特に京都大学は,問題に誘導がほとんどないため,自分で最初から最後までの解の道筋を作っていかなければなりません。この力は,パターン問題を処理できる力だけでは足りず,そのような典型問題に当てはまる形に目の前の問題を変形ないし解体して,解いていかなければなりません。そのためには,ぜひ根本的な理解を大切にして学習に取り組まれると良いと思います。
あるテーマをきちんと理解できたかの一つの目安は、東大のレビュー記事にも書きましたが,その内容を他人に分かりやすく説明することです。もし不安があるのであれば,ぜひいま一度教科書を確認するなど,あやふやな部分をつぶしていきましょう。そのような基本に忠実な学習が,「応用力」を養ってくれます。
それでは今回はこのへんで!
少人数制 大学受験専門
学習塾Dear Hopeへのお問い合わせ、体験授業のお申込みはこちらからお願いします。
