2021年 早稲田大学 理工学部(数学)入試問題 最新レビュー
こんにちは。学習塾Dear Hope 数学・物理担当の伊藤です。
前回に続き,最新入試問題の紹介です。
今回は早稲田大学・理工学部の数学を取り上げます。
早稲田大学・理工学部の数学のセットは5問あり,出題テーマは以下の通りです。出題数や試験時間は例年と同じです。
第1問 3次曲線上の点を通過する2本の直線のなす角と,その角の最小値
第2問 高次式を特定の4次式で割ったときの余り
第3問 複素数平面の直線上の点zに対し,点z2の存在領域
第4問 n個の箱の中にk個の玉を無作為に入れ,各箱に入った球の個数の最大値と最小値の差に関する確率
第5問 正四面体とその底面の外心を中心とする球との共有点等の位置
私個人としては,全体的に昨年よりも易化したと感じます。いつものように独断と偏見で難易度を付けると,次のようになります。
(易)2≦1<3≦5<4(難)
以下,詳しく見ていきます。
《第1問》
xy平面上の曲線y=x3上の2点A(-1,-1),B(1,1)と,原点OとBとの間を動く点P(t,t3)の3点をとり,直線APと直線PBとのなす角の最小値を求めさせる問題です。
誘導に従ってx軸と直線APおよびPBとのなす角をそれぞれtを用いて表し,さらにtan∠APBをtの関数として表すことにより,関数の最大・最小問題に帰着させるタイプの問題です。特にひねっている箇所もなく,ここはスムーズに処理したい問題です。
《第2問》
整式の割り算です。
(1)と(2)は,x6とx2021をf(x)=x4-x2+1で割った余りを求める問題です。A3+B3の因数分解の公式から,f(x)・(x2+1)=x6+1であることに気づければ容易です。
(3)はnが3の倍数のとき,(x2-1)n-1がf(x)で割り切れることを証明させる問題です。f(x)の式を,x2-1=x4-f(x)と見て,(1)の結果と合わせて考えることにより終了です。
《第3問》
複素数平面上の2点A(α=2+ⅰ),B(β=-1/2+ⅰ)が与えられ,(1)ではα2,β2および原点Oの3点が一直線上にあることを証明します。これはα2/β2が実数になることを言えばOKです。
(2)はzが直線AB上を動くときのz2の軌跡を,(3)はzが△OABの周および内部にあるときのz2の存在領域を,それぞれ求めさせる問題です
(2)はz=k+ⅰなどと置き,パラメータkを消去すれば容易に求めることができます。
一方,(3)は,存在領域の概形を推測することはそれほど難しくありませんが,記述しにくい問題でした。基本的には,予選決勝法に従えばよく,例えば,領域内の点のうち,Im(z)=k(kは0≦k≦1をみたす定数)である点のみに注目して(つまりkを固定して),そのときz2が描く軌跡に注目すると良いでしょう。その際,f(x,y)=0により表される図形を原点Oを中心としてx軸方向にa倍,y軸方向にb倍した図形はf(x/a,y/b)=0により表されるという事実に注目するとスムーズです。
第4問は後述します。
《第5問》
早稲田らしい空間図形の問題です。正四面体とその底面の外心を中心とする球との共有点等の位置をベクトルにより求めていく構成です。この共有点の位置は比較的容易に得られますが,この他に,球と正四面体の側面との共有部分(円弧)の中心の位置を特定させる問題も含まれており,ここをうまく処理できるかがポイントになります。
この円弧の中心は,球から四面体の側面に下した垂線の足に一致することに気づく必要がありますので,このあたりは立体図形の問題をどれくらい練習してきたかで差がついたと思います。また,垂線の足を求めるわけですから,正射影ベクトルが活躍します。
先日紹介した慶應義塾大(理工学部)の問題でも正射影ベクトルを利用するとスムーズに処理できる問題が出題されていましたので,やはり難関大を目指す皆さんにおいては,正射影ベクトルをきちんと使いこなせるようにしておくことが必要だと思います。
さて,第4問については,少し詳しく見ていきたいと思います。本問は,確率の基本的な計算手法を理解できているか否かを問う問題です。
まず,問題文を引用します。

(出典:2021年度 早稲田大学(理工)第4問)
本問は,確率の考え方をきちんと理解している人にとっては難しくありませんが,公式の暗記で乗り切ってきた人にとっては,どの考え方を適用したらよいのか迷ってしまったかもしれません。教科書レベルの話になりますが,いま一度,確率の考え方を確認しておきましょう。
(1)~(3)のいずれも,本質的には同じ問題ですので,ここでは(3)のP2(3個の玉を3個の箱に入れるとき,箱に入っている玉の最大値-最小値=2のとき)について考えてみましょう。要するに,3個の玉が2個と1個に分かれていずれかの箱に入る確率です。
本問は,余事象による(P1=1-P0-P2-P3により求める)のが最も効率的だと思いますが,確率計算の理解を深めるため,直接求めてみましょう。また,簡単のため,n=3とします。
まずは誤答を2つ示します。どこに誤りがあるか,考えながら読んでみてください。
(誤答1)
3個の玉を3個の箱に入れる方法は,3個の玉と2本の仕切りの順列で考えることができるから5C3=10(通り)。
このうち,3個の玉が2個と1個に分かれる場合の数は,2個の玉をひとまとまりとして考え,2つの玉(このうち1つの玉は2個の玉のまとまり)と2本の仕切りの順列で考えることができるから,4C2=6(通り)。
ゆえに求める確率は,
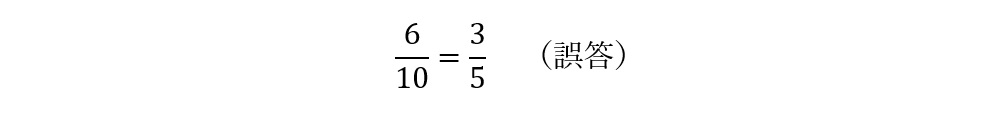
(誤答2)
1個目の玉はどの箱に入っても良いからその確率は1。2個目の玉は1個目の玉と同じ箱に入ればよいから,その確率は1/3。3個目の玉は残り2つの空箱のどちらかに入ればよいから,その確率は2/3。
ゆえに求める確率は
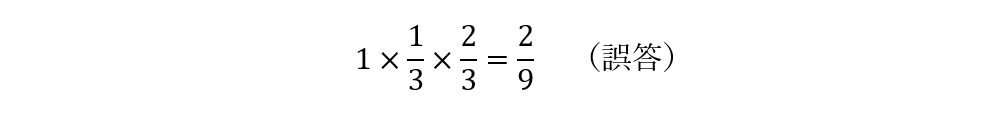
次に,正しい答えを示します。
(正答)
玉と箱をすべて区別して考える。
まず,全事象は33=27(通り)。
次に,玉が2個と1個に分かれる場合は,同じ箱に入る2つの玉の決め方が3C2=3(通り),2個の玉と1個の玉とを区別のある3個の箱に入れる方法は,3P2=6(通り)。
ゆえに求める確率は,
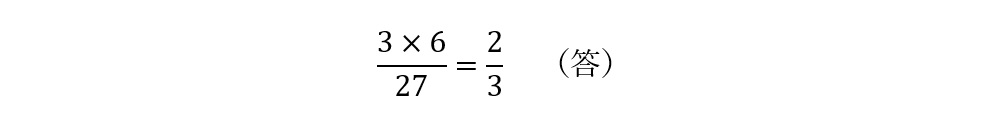
(誤答1)と(誤答2)に共通する誤りは,玉と箱をきちんと区別していないことにより,全事象に対して,注目している事象がどれだけ起こりやすいかが正確にカウントされていない点です。
この点は確率と個数の処理との決定的な違いで,極めて重要です。分かっている人にとってはごく当たり前のことです。しかし,残念ながらこの点を正確に理解できていない生徒さんが多いのが実情です。
簡単のため,次の例題を考えてみましょう。
(例題)
赤玉4個,白玉2個が入った袋から3つの玉を取り出すとき,赤玉2個と白玉1個を取り出す確率を求めよ。
(解答例)
赤白あわせて6個の玉から3つを選ぶ方法は,6C3=20(通り)。
4個の赤玉から2個を取り出す方法は4C2=6(通り),2個の白玉から1個を取り出す方法は2C1=2(通り)。
ゆえに求める確率は,
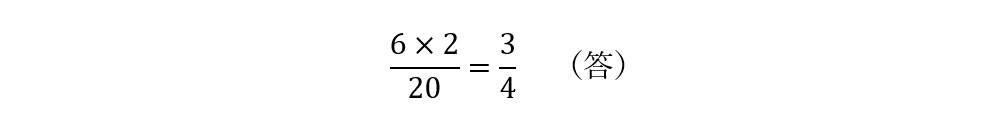
おそらく,皆さんも普段このように解いていると思います。
では,この例題を次のように考えるとどうでしょうか。
(誤答)
赤白あわせて6個の玉から3つを選ぶ方法は,「赤赤赤」「赤赤白」「赤白白」の3通り。
このうち,赤玉2個と白玉1個を取り出す場合は「赤赤白」の1通り。
ゆえに求める確率は,1/3(誤答)。
この考え方が正しいとすると,赤玉10000個と白玉2個が袋に入っていても,全事象が「赤赤赤」「赤赤白」「赤白白」の3通りになってしまい,必然的に確率も同じ1/3になります。
しかし,これは明らかに変です。赤玉10000個に対して白玉が2個しか入っていないのであれば,「赤赤白」となく確率は1/3よりもずっと小さくなるはずです。
この原因は,それぞれの玉を区別していないことにあります。区別が無いと,「赤赤白」が他の色の出方に比べてどの程度出やすいのかが,全く考慮されません。
さて,解答例では,
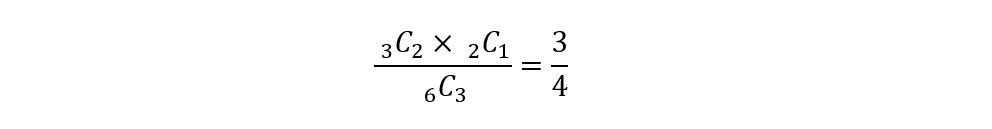
として答えを求めました。
この式に含まれる6C3は,「異なる6個のものから3個を選ぶ場合の数」を表します。
「異なる」
の部分がポイントです(そうだっけ?と思った方は,ぜひ教科書で確認しましょう)。すなわち,みなさんが普段使っているこの計算式では,実は6個の玉をすべて区別して考えていたわけです。
このように,確率では基本的に分母と分子の場合の数を計算するにあたって,対象物をすべて区別して数え上げる必要があるのです。
この点の理解はとても大切ですので,あやふやだった方はぜひこれを機に理解を深めていただければと思います。
ちなみに,(誤答2)で示した解答は,箱だけが区別されていますので,あとは玉を区別して考えればOKです。すなわち,区別のある玉を2個と1個のグループに分ける方法は3通りあるから,これを掛けると, 2/9×3=2/3となり,正答と合致します。
いかがでしたでしょうか。
今回は,確率の初歩的な考え方をおさらいしました。参考になれば嬉しいです。
それでは今回はこのへんで!
