伊藤 大幸

こんにちは。学習塾Dear Hope　数学・物理担当の伊藤です。

前回に続き，2021年の最新入試問題の紹介です。

今回は「正射影ベクトル」にスポットを当てて，

①慶応義塾大学　経済学部　第5問，
②慶應義塾大学　理工学部　第5問，
③早稲田大学　理工学部　第5問

の問題を取り上げます。

これらの大学・学部の入試問題を通して印象に残ったことの１つに，「正射影ベクトル」の考え方を理解していると余裕をもって合格できた可能性が高い，ということが挙げられます。というのは，ここで紹介する問題が合否を分けた可能性が高いからです。

「正射影ベクトル」と聞くと難しそうに感じられるかもしれません。しかしこれは，内積の意味が理解できていれば難しくありません。

入試問題を検討する前に，まず「内積」と「正射影ベクトル」について簡単に説明します。

〔内積〕

教科書に記載のとおり，内積は次の式で定義されています。

詳しくは省略しますが，この定義は余弦定理との整合を図るために決められています。

さて，この式を次のように変形してみましょう。

次の図に示すように，[1]の内積の定義式は，線分OAと，OAに対する線分OBの正射影（直線OAに対し垂直に落とした影OH）との積を表しています。

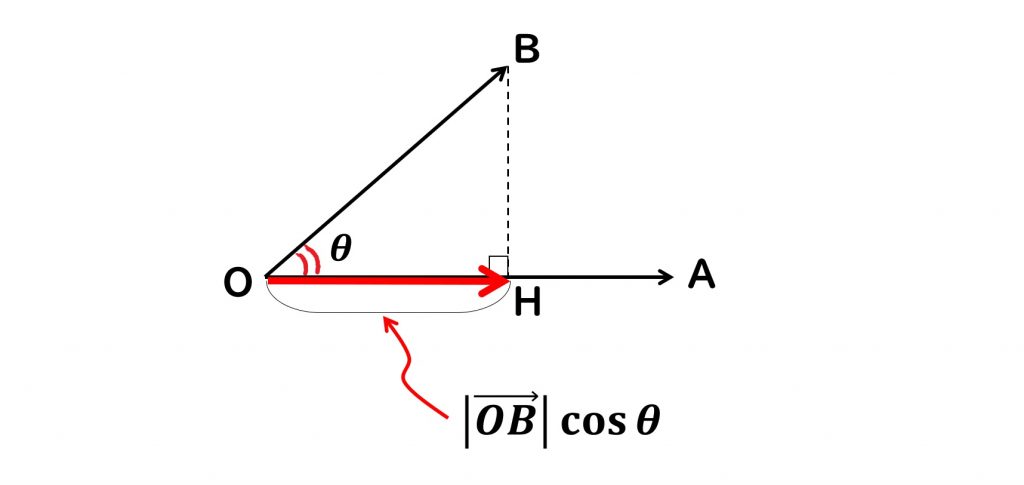
この積は，OAとOBとのなす角が鋭角（正射影がOAと同じ向き）のとき，プラスになります。一方，OAとOBのなす角が鈍角（正射影がOAと逆向き）のとき，マイナスになります。また，OAとOBが直交するときは０になります。

影を映す直線OAは，いわばスクリーンと言えますから，内積とは，

スクリーン（線分OA）×影（OH）

を表しています。また，この内積の符号により，OAとOBとのなす角が鋭角か，鈍角か，直角か，が分かるようになっています。

〔正射影ベクトル〕

式[1]を次のように変形してみましょう。

式[2]は，先の図から分かるように，影（OH）の長さと，スクリーンに対する影の方向（正か負か）とを表しています。

したがって，これにベクトルOAの単位方向ベクトルを付加した式は，ベクトルOHに他なりません。すなわち，

これが正射影を表すベクトルということで，「正射影ベクトル」と呼ばれています。

特に，スクリーンの長さ（OAの長さ）が１の場合は，

となり，例えば次の一橋大学の問題のように出題されます。

（出典：2019年度　一橋大学　第２問）

題意より，OQ＝１ですから，

「点Pは，ベクトルOAを直線OQに正射影したベクトルの終点である」

ということが分かります。

すなわち，常にOP⊥APという関係が成り立つため，点Pは「線分OAを直径の両端とする円」の上に存在することが分かります。よって，ｘ，ｙの変域から，求める軌跡は，この円のうち，第１象限およびｘ，ｙ各軸上に存在する部分であると結論付けられます。

以上の知識をもとに，今年の早稲田・慶応の入試問題を見ていきましょう。

＊　　＊　　＊

１問目は，慶應義塾大学・経済学部の問題です。以下に，問題を引用します。

（出典：2021年度　慶応義塾大学　経済学部（第５問））

本問では，次の図のように，球Sの接平面上に3点A，B，Cが配置されています。球Sと接平面との接点は点Aですので，直線OAと接平面とは直交しています。

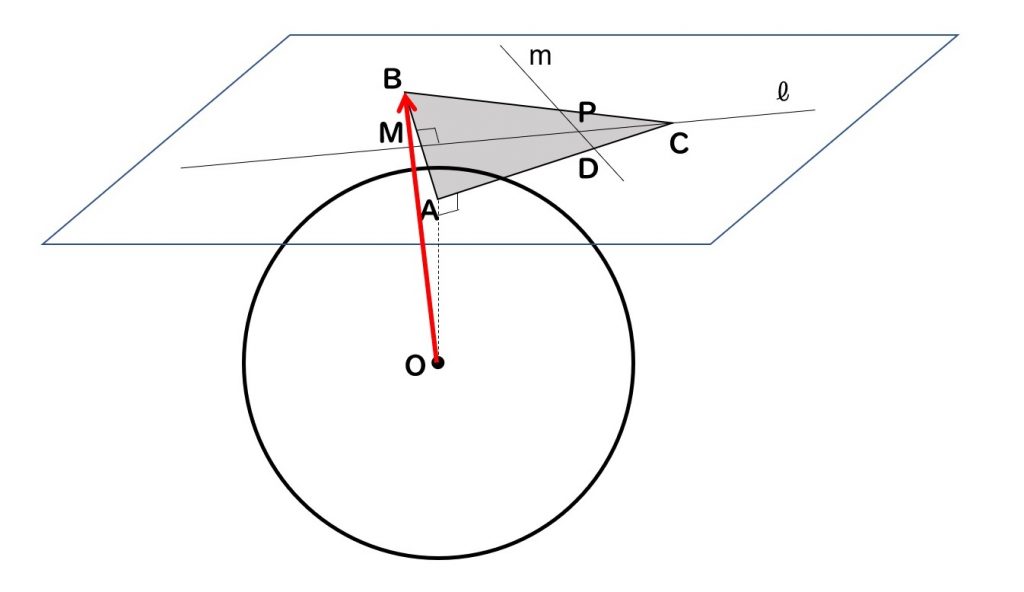
さて，まず（１）を見てみましょう。２つのベクトルOAとOBとの内積が問われています。

内積は，「スクリーン×影」でしたね。

OAをスクリーンとすると，図より，OAに投影したOBの影は，OAに一致することが分かります。また，スクリーンと影（＝OA）は同じ向きですから，求める内積は，

OA×OA＝４

となります。

さらに，問題文の冒頭で，２つのベクトルAB，ACの大きさと，内積とが与えられています。これらの情報から，三角形ABCがCA＝CBの二等辺三角形であることが分かります。

その理由は次の通りです。すなわち，ベクトルABとACの内積が２ａ^２であり，ABの長さが２ａであることから，ベクトルABにACを投影すると，その影はベクトルABと同じ向きであり，その長さはａになるはずです。

ということは，線分ABの中点をMとすると，ACの正射影はAMに一致することになるため，辺ABの垂直二等分線（直線ℓ）は点Cを通ることが分かります。底辺の垂直二等分線が頂点を通る三角形は，二等辺三角形ですね。

このように，問題の意味を考えて△ABCと直線ℓとの関係を事前に解析しておくと，（２）において△CDP∽△CMAから，CP：PM＝３：５であることがすぐに分かり，

を得ます。

＊　　＊　　＊

2問目は慶応義塾大学・理工学部の問題です。まず，問題文を引用します。

（出典：2021年度　慶応義塾大学　理工学部（第５問））

本問では，（３）において正射影ベクトルを利用するとスムーズです。

先に図を示します。

（３）では，２点Q，Sそれぞれの座標（位置ベクトル）を求めたいですね。

図より，ベクトルOQは，ベクトルｕ（スクリーン）に対してOPを正射影して得られるベクトルです。したがって，

となり，２点Q，Sの座標が特定されます。ここまで来れば，あとはよくある計算処理で答えを求めることができます。

＊　　＊　　＊

最後は，早稲田大学・理工学部の次の問題です。

（出典：2021年度　早稲田大学　理工学部（第５問））

ここでは，（１）のベクトルOGを求めてみます。本問では，これを求められるかで全体のでき具合が決まります。

まず，関係する部分のみ，図を示します。本問では，このような図をスケッチできるかも大きなポイントです。

この図において，平面αは3点O，D，Eを含む平面です。問題文に記載されている「弧DEを含む円周」とは，平面αと球との共通部分（交円）です。当然，この交円上に点Aおよび点Bも位置しています。

さて，図より，ベクトルOGは，半直線OG（赤の破線）に対するOMの正射影ベクトルです。したがって，半直線OGの方向ベクトルをスクリーンとして，これにOMを投影します。

対称性より，半直線OGは∠AOBの二等分線ですから，その方向ベクトルは，

としてよいでしょう。

また，正四面体の性質から，点Mは△ABCの重心に一致するため，

となります。ゆえに，先に紹介した正射影ベクトルの考えによれば，ベクトルOGは，次のように表されます。

ここで，△OAB，△OBC，△OCAの一辺の長さをdとすると，

を得るから，結局，

と，あっという間に求まります。

＊　　＊　　＊

いかがでしたでしょうか。
今回の記事では，2021年度の最新の入試問題から，早稲田大学と慶應義塾大学の正射影ベクトルに関する問題を取り上げました。もちろん，他の大学や過去の入試問題を紐解くと，同様の問題は，枚挙にいとまがありません。

ベクトルの問題で「垂直」という条件が出てきたら，基本は「内積＝０」なのですが，これに加えて，「正射影ベクトルが利用できないか？」という視点で問題を分析してみると，簡単に答えにたどり着ける問題が多く見つけられるでしょう。意欲的な皆さんは，ぜひマスターされてください。

それでは今回はこのへんで！