伊藤 大幸

こんにちは。
全国オンライン／品川区武蔵小山
学習塾 DearHope　数学担当の伊藤です。

今回は、2020年度　東京工業大学の数学の入試問題についてレビューします。

結論から言うと、原理原則の理解を問う基本に忠実な問題だな、という印象です。

まず、全体の問題構成から見ていきましょう。

例年どおり大問５題の構成で、出題テーマは以下の通りです。

私個人の独断と偏見で難易度をつけると、２＜３＜１＜４＜５　です。

昨年と比較して解きやすいセットだったので、１～３はしっかりと得点して、４，５で勝負、といったところだと思います。

第１問では セオリー通りに約数に注目することがカギ であり、

第２問では 正三角形を構成する条件という超頻出のテーマ  が出題され、

第3問では 中学で学習する「方べきの定理の逆」を利用させる出題 でした。

第3問のように、中学で学ぶ定理（方べきの定理の他には、「中点連結定理」、「円周角の定理の逆」など）を利用する問題が大学入試において出題されるのは、実はよくあることです。このあたりはしっかりと復習をしておきましょう。

さて、冒頭で、今年の東京工業大学の数学のセットは「基本に忠実」だった、と述べました。

これについて、上述した第１問～第３問に加え、今回は特に、第４問について見ていきたいと思います。

2020年 東京工業大学　数学第４問　解説

以下、第４問を引用します。

本問は、いわゆる「斜回転体」 （回転軸がｘ軸・ｙ軸に対して傾斜している回転体） の求積問題であり、出題自体は特に珍しいものではありません。

では、この問題のどこが印象的だったのかというと、難関大を目指す理系の皆さんにとっておなじみの「傘型分割によるパップス・ギュルダンの定理を用いた求積」を阻止している点です。

そもそも、パップス・ギュルダンの定理（体積＝断面積×重心の移動距離）は、教科書の範囲外であり、きちんと証明できる高校生はほとんどいないと思います。そういう背景もあって、本問では原則どおりの処理を求めたのだと思います。

斜回転体の求積問題では、回転軸がｘ軸に対して傾斜しているため、教科書で紹介されている体積Vの公式

をそのまま利用することができません。

しかし、この公式が述べている基本原理をきちんと理解していれば、本問は難しくありません。この基本原理とは、「断面積をその法線方向に積分すると体積が得られる」ということです。本問はまさに、この原理に忠実に解くことを求めているのです。

では、さっそく見ていきましょう。

まず（１）です。ｎが奇数なので、回転される図形は、図１に示す正弦曲線とｘ軸とで囲まれた部分です。

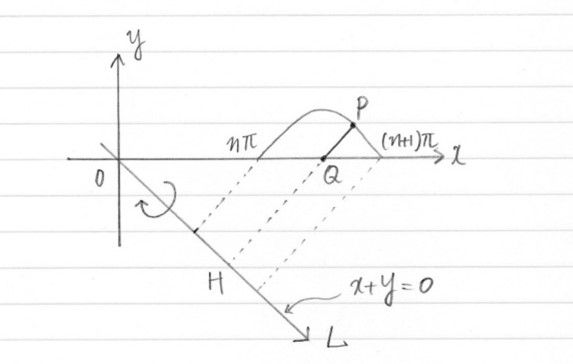
まず、問題を解くために必要な座標を求めておきます。図１に示すように点Hを定めると、直線PHの方程式を踏まえ、

となります。（１）で求めるべきは、要するに、図１に示す太線部PQを回転軸周りに1回転させてできるドーナツ形の図形（図２）の面積です。

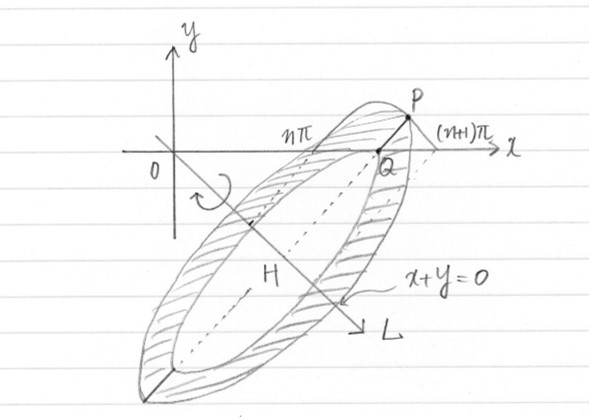
これは、外側の円の面積から内側の円の面積を引けばよく、

となります。

さて、（２）に移ります。（１）の結果を利用しなさいという指示がありますから、パップス・ギュルダンの定理を使うわけにはいきません。よって、原則どおりに処理していきます。すなわち、（１）で求めた面積は、「回転体を平面ｙ＝ｘで切断したときの断面積」ですから、この断面積をその法線方向である「回転軸線L」に沿って積分すればよいわけです。

ゆえに、体積Vは、

となります。式［1］において、積分変数はLですが（積分はL方向に行いますが）、被積分関数はｘで定義されています。このため、単純に被積分関数のみを積分するわけにはいきません。この点が、本問で最も注意しなければならない点です。

ここでは、次の2つのうちのどちらかの道筋にしたがい計算を進めていきます。

（ⅰ）　ｘをLに書き換える。

（ⅱ）　Lをｘに書き換える。

どちらが良いかを判断するため、ｘとL（＝OH）の関係式を確認しましょう。図１、２より，

が成り立ちますから、（ⅱ）の方がよさそうですね。

道筋がきまったら、あとは計算あるのみです。式［2］はxとLについて恒等的に成立する式ですから、微分しても等号は成立し、dxとdLについて以下の関係式を得ます。

さらに、積分区間については、L：α→βのとき、x：(n－1)π→nπです。よって、体積Vの式は、以下のように書き換えて計算することができます。

以上のように、原則どおりに体積Vの式を立て、被積分関数に用いられている文字（ｘ）と積分変数（L）とのズレをそれらの関係式に基づいて整えればよいわけです。難易度の高い問題では、このような「2つの変数の中継プレー」がカギになることがあります。

傘型分割により、パップス・ギュルダンの定理を用いて体積を求めることは確かに有効です。しかし、そのような応用テクニックは、基本原理の理解あってこそ、なのです。

同様に、ｙ軸周りの回転体に関する求積問題で、バウムクーヘン分割を利用することもよく知られているテクニックです。私もよく利用します。

これについても、まずはｙ軸まわりの回転体の体積Vが、

により得られるという原則を押さえた上で利用されることをお勧めします。

傘型分割も、バウムクーヘン分割も、習いたての頃は嬉しくてやたら使いたがるものですが（私もそうでした）、問題に慣れるにつれ、原則どおりの式も悪くないな（むしろそちらの方がラクなケースもある）と感じてくることでしょう。

さて、東京工業大学　第４問のポイントは、被積分関数の変数（x）と積分変数（L）とが異なっていても、それらをつなぐ関係式さえあれば処理できる、ということでした。

このことは微分についても言えます。

関連する問題として、2007年　慶応義塾大学（医学部）第3問　をご紹介します。

2007年　慶應義塾大学（医）数学第３問　解説

まず問題文を引用します。

本題は（３）ですので、（１）と（２）は要点のみ示します。

（１）は、誘導にしたがって計算を進めればよく、次式を得ます。

次に（２）です。まず、絶対値の中身の関数をg(y)とおくと、a≦0のときとa≧1のときは、区間0≦y≦1においてg(y)が一意に定まるため、

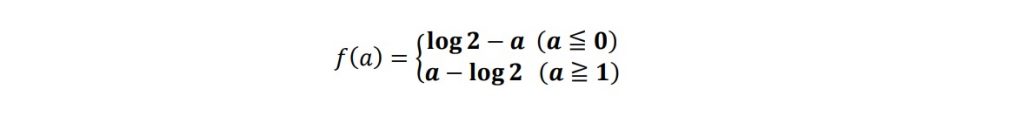
となります。

一方、0≦a≦1において、g(y)は、y＝tの前後で符号が変化します。具体的には、y≦tのときg(y)≦0、y＞tのときg(y)＞０です。ゆえに、

続いて（３）です。（２）から、ｆ(a)は、a≦0のとき単調に減少し、a≧1のとき単調に増加しますから、0≦a≦1の範囲で最小値をとることが分かります。

つまり、0＜a＜1におけるf(a)の式を微分し、増減を調べていくわけです。

しかし、計算してみるとわかりますが、とても煩雑で机をひっくり返したくなると思います。試験時間から、本問にかけられる時間は25～30分程度ですから、簡単に処理できるのであればそうしたいところです。

さて、今計算しようとしているのは、「df(a)／da」です。これを求めるにあたり、aで微分する以外に方法はないのでしょうか。

実は、もっと容易な方法があります。合成関数の微分の式から、

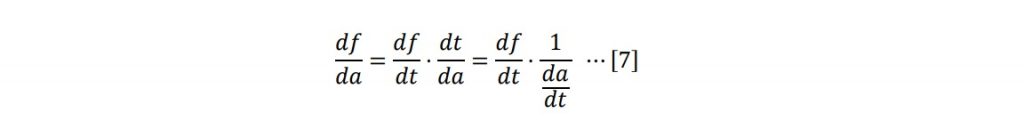
が成立します。すなわち、aではなくtで微分しても結論が得られます。

このことは、（２）の途中式

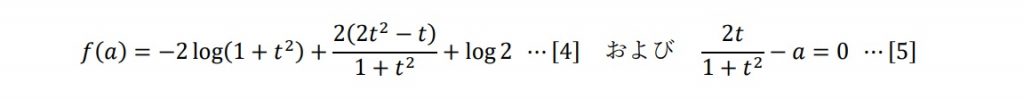
から着想を得ることができます。

つまり、aとtは式［5］で結び付いているから、aで微分する計算をtで微分する計算に変換することができる、ということです。このような中継プレーを利用する点で、本問は、先に挙げた東京工業大学の問題と通じるものがあります。

さて、f(a)はtで容易に微分でき、

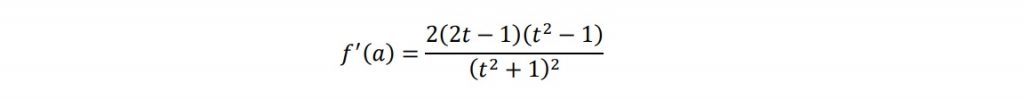
これより、0＜a＜1においてf’(a)＝0を満たすaの値は、ｔ＝1/2からa＝4/5となり、このときf(a)は最小値

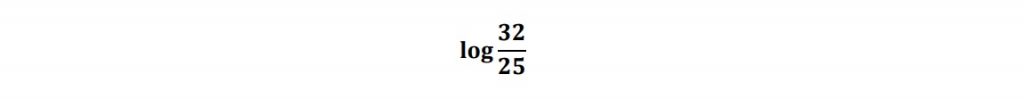
をとります。

もちろん、厳密には「da/dt」の符号を考慮する必要がありますが、設問が穴埋めの形式であることを踏まえ、a≦0とa≧1におけるf(a)の増減を考慮すると、「df/dt」のみを考慮すれば十分でしょう。

以上、２つの入試問題からお伝えしたいことは、教科書外のテクニックも役立つ場面は多くありますが、最後に頼りになるのは「原理原則についての正確な理解」です。テクニック自体を否定するつもりは全くありませんが、基本原理について理解できていることは高いレベルで実力を安定させることにつながると思います。

テクニック至上主義になりがちな方は、ぜひ、足元が固まっているか確認されることをお勧めします。

それでは今回はこの辺で！

少人数制　大学受験専門
学習塾Dear Hopeへのお問い合わせ、体験授業のお申込みはこちらからお願いします。