2024年度入試 東京工業大学(数学)レビュー:深い理解に加え、計算力と記述力がモノをいうセット
こんにちは。品川区にある大学受験のための少人数制の学習塾「Dear Hope」副塾長の伊藤です。
今日は,先日実施された国立大の入試から,東京工業大学の数学について所感など記していきたいと思います。
平易な問題は少なく,馬力(計算力や記述力)が求められる問題でした。総じて記述量が多く(その分試験時間も長いですが),かつ,小手先のテクニックが利かないタイプの問題であり,個人的には解いていてとても面白く感じました(しかし,試験となるとそうも言っていられませんね)。
まず,今年のセットは次の通りです。
(第1問) 放物線とその軸に接する円の中心の軌跡と,その軌跡の接線に関する問題。
媒介変数を用いて表された関数の微分がテーマです。
(第2問) 媒介変数を用いて表された関数について,極限や曲線の長さを求める問題。
(第3問) 2つの直線上に定められる点列の極限に関する問題。
(第4問) 表が出る確率が互いに異なるn枚の硬貨を用いた確率の問題。
漸化式により確率を求める問題で,最後の(3)では,極限値が問われました。この極限値には,自然対数の底eが関係しました。
(第5問) 与えられた二次方程式の解αに対して,αn=1となる正整数nが存在する条件を求める問題。
独断と偏見による難易度としては,
(易)5<1=3<2<4(難)
だと思います。第5問は確実に完答し,第1問と第3問もぜひ完答し,残り2問のうちどちらかで勝負,といったところだと思います。
以下,いくつかの問題を引用しつつ,コメントしたいと思います。
(第1問)

(出典:2024年度 東京工業大学入試問題 数学 第1問)

では,実際に解いてみましょう。
とりあえず,Saの中心の座標を(X, Y)とおき,X,Y,aの間に成り立つ関係式を導きましょう(題意より,X, Yはともに正です)。
Y軸と円の中心との距離(Xであり,これは正)が,円の中心と接点との距離に等しく,かつ,円の中心と接点とを結ぶ直線と接線(傾きは微分により,a)が直交するから,

①を二乗し,②の分母を払って整理すると,a>0,X>0,Y>0の条件のもとで,
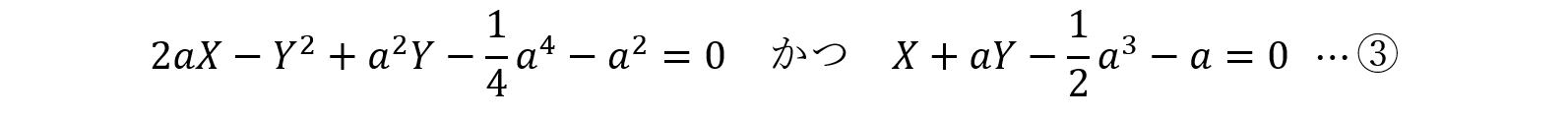
ゆえにa=1のとき,上式は
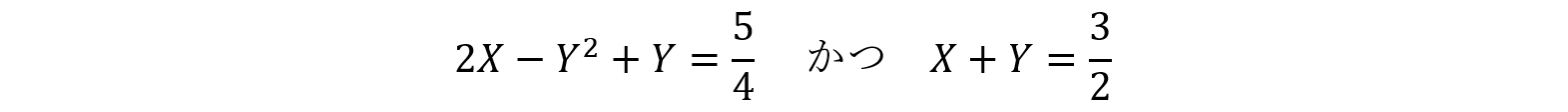
これを満たす正のX,Yは,次の通りです。
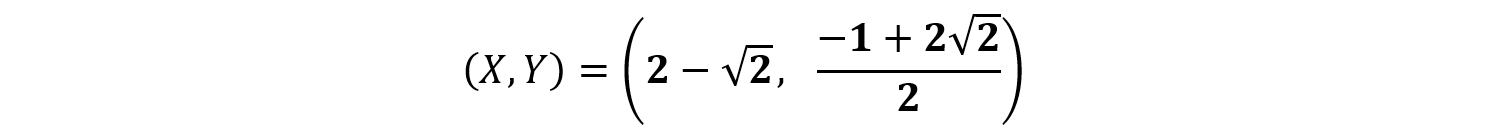
次に(2)です。これは要するに,
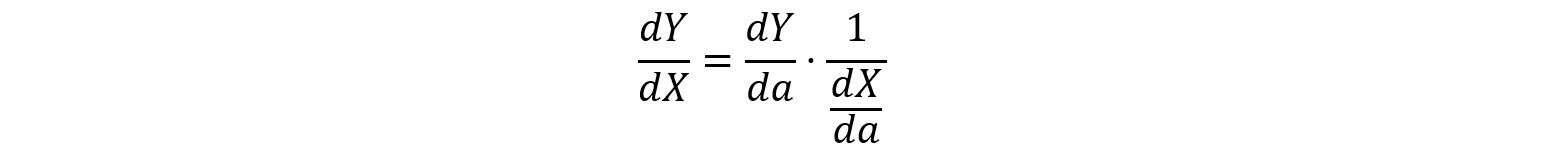
において,a=1のときの値を求めればOKです。
③の式をaで微分していきましょう。

ゆえにa=1のとき,上式は
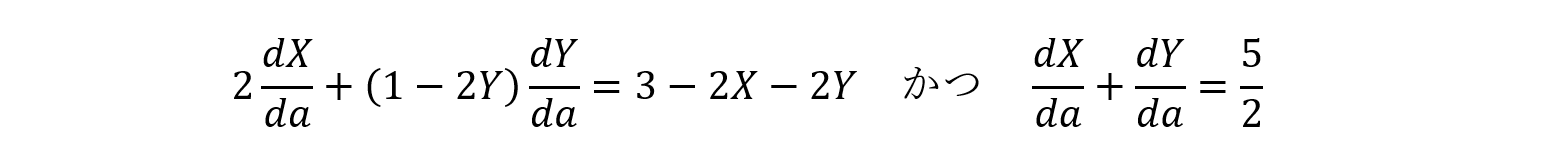
ここで,a=1のとき,X,Yは(1)で求めた通りだから,第1式の右辺「3-2X-2Y」は0。ゆえに,この第1式より,以下の答えを得ます。
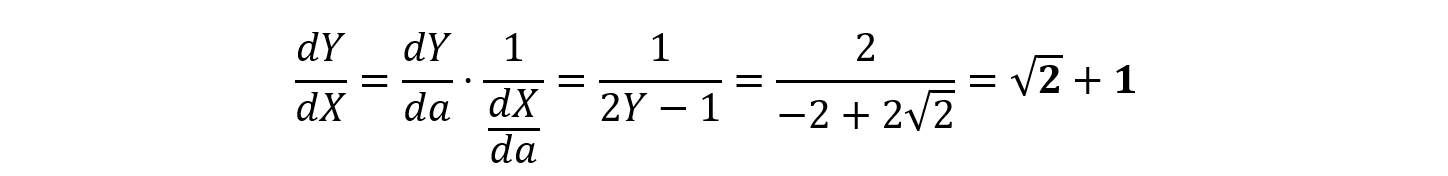
もちろん,(1)の段階で,XとYを直接aを用いて求めてもよいのですが,上記のように,その前段階の式を使って処理する方が計算ミスも防げるため望ましいように感じます。
続いて,第4問を検討します。
(第4問)

(出典:2024年度 東京工業大学入試問題 数学 第4問)
本問は,漸化式を立てるとスムーズです。(1)を解いてみましょう。
考えるべき事象は次の2つです。2以上のnに対して,
・Cnが表のとき,C1~Cn-1のn-1枚の硬貨のうち偶数枚が表。
・Cnが裏のとき,C1~Cn-1のn-1枚の硬貨のうち奇数枚が表。
ゆえに,
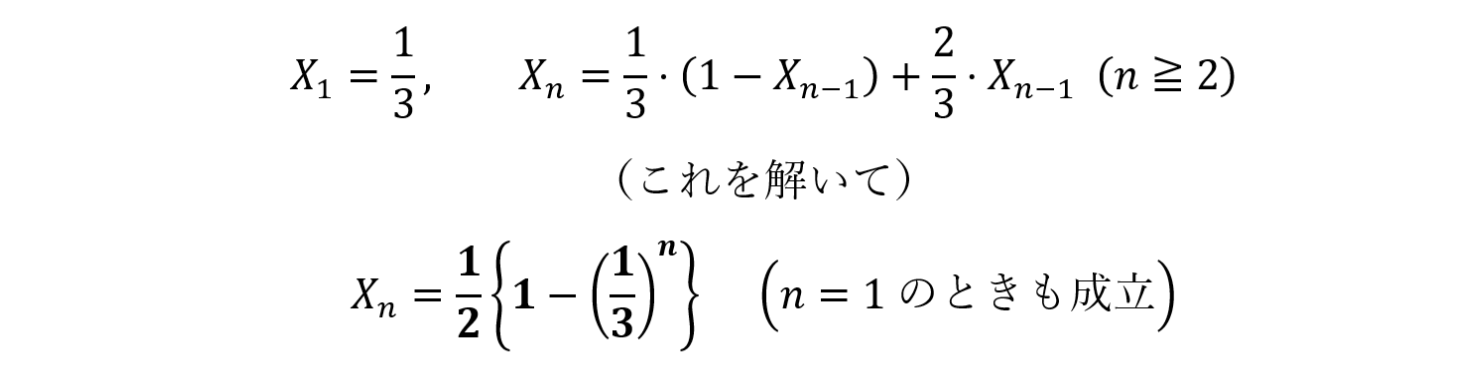
(2)も同様に考えると,
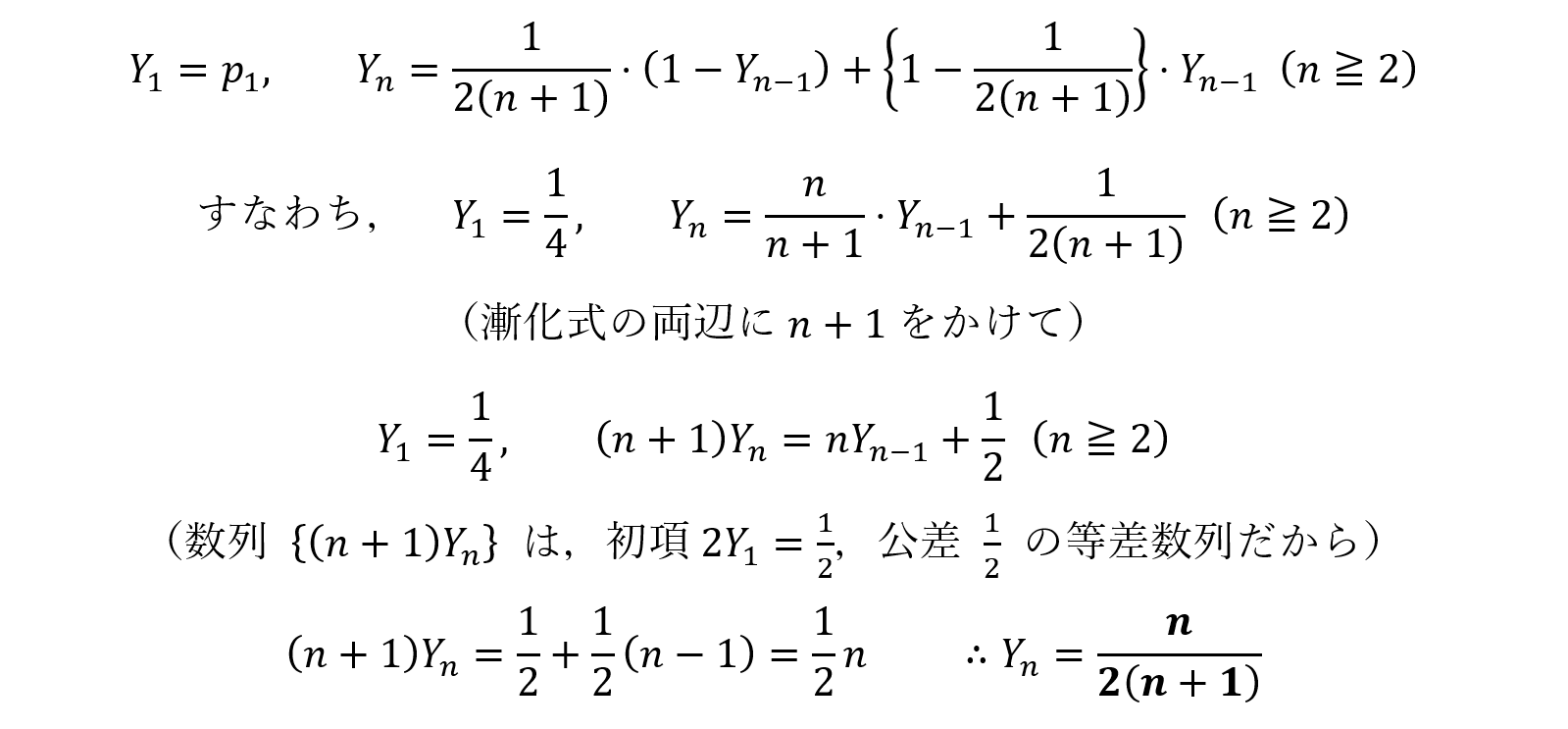
さて,ここまでは普通の確率の問題ですが,最後の(3)は手数が多く,少し難しいです。まずは(1),(2)と同様に,s回の試行の結果,偶数枚の硬貨が表となる確率をasとし,これが満たすべき漸化式を書き表してみましょう(「s回」のように,m以外の文字を用い,漸化式を解いた後にs→mと置き換えます。なぜなら,漸化式を処理する場面では,mは定数だからです。mを用いると,混乱の原因となります。大切なポイントです!)。
本問では,3グループある「m枚の硬貨のカタマリ」の中では,表が出る確率は等しいため,ここでは表が出る確率を一定の「p」として立式します(したがって,(1)と同じタイプになります)。
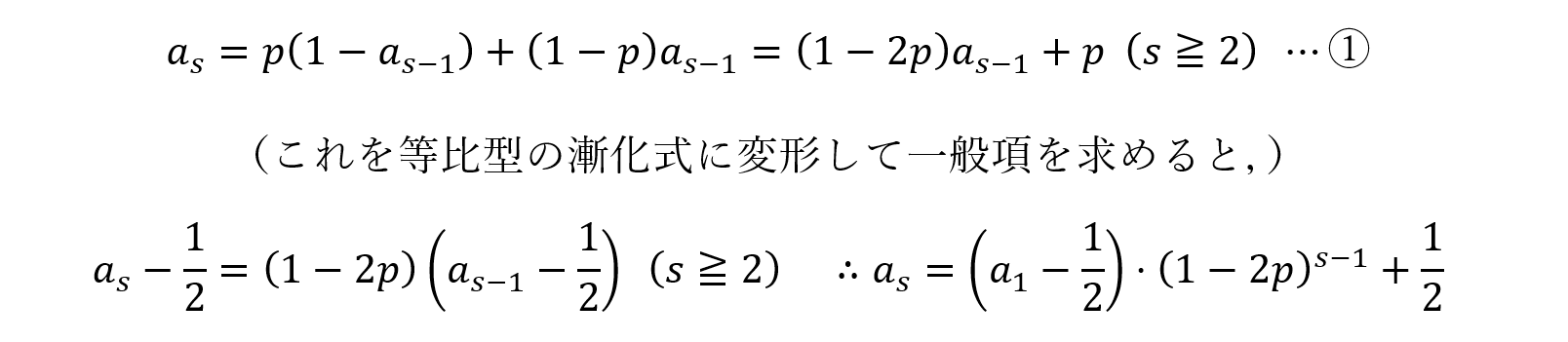
この結果によれば,
・k=1, 2, …, mにおいて,表となる硬貨が奇数枚となる確率Amは,
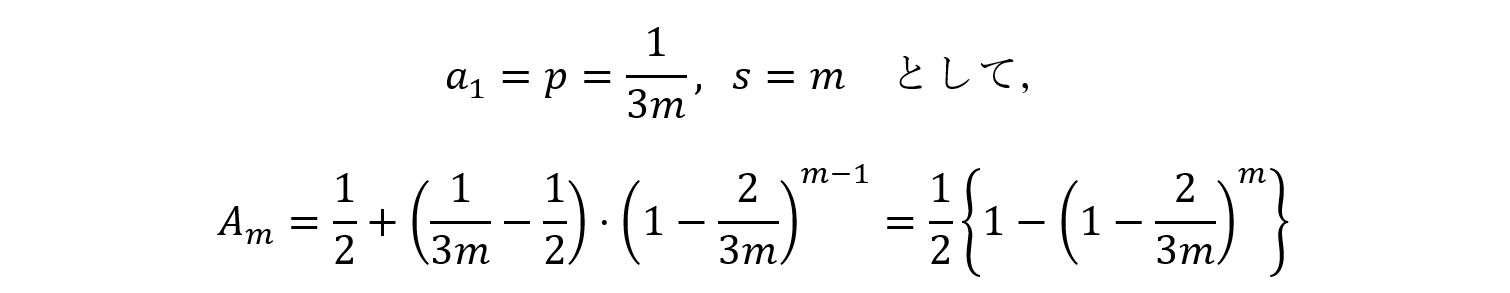
・k=m+1, m+2, …, 2mにおいて,表となる硬貨が奇数枚となる確率Bmは,
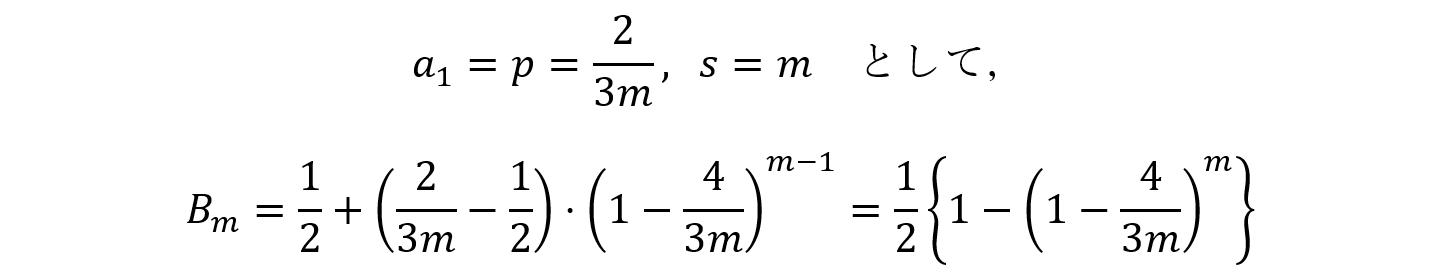
・k=2m+1, 2m+2, …, 3mにおいて,表となる硬貨が奇数枚となる確率Cmは,
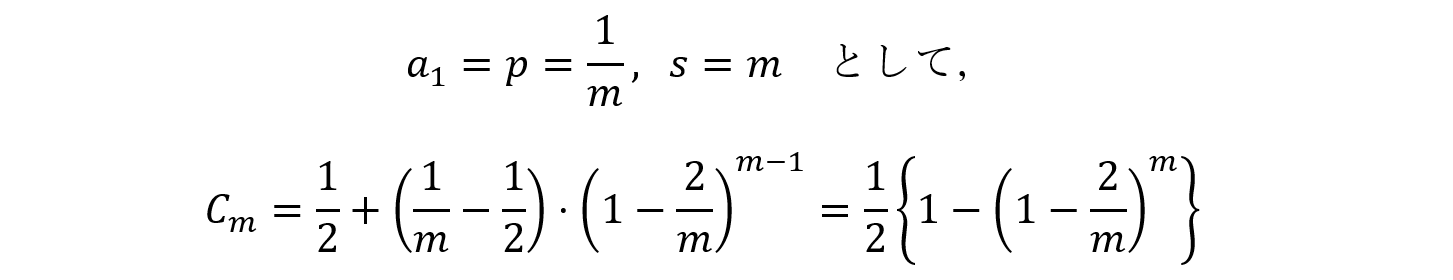
最後に,Z3mを求めましょう。以上の3つのグループにおいて,表が出る硬貨の偶奇は,
・偶数のグループが2つと,奇数のグループが1つ,あるいは,
・奇数のグループが3つ のいずれか
であればよいから,
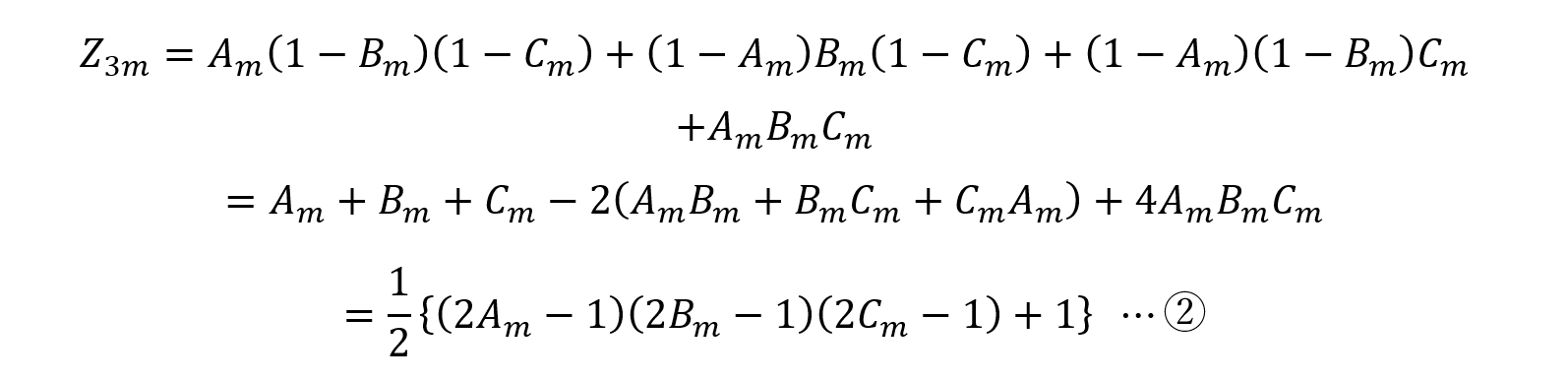
と表すことができます。
さて,この式にAm, Bm, Cmを代入してもよいのですが,煩雑になるので,あらかじめm→∞のときの極限値をそれぞれ求めておきましょう。
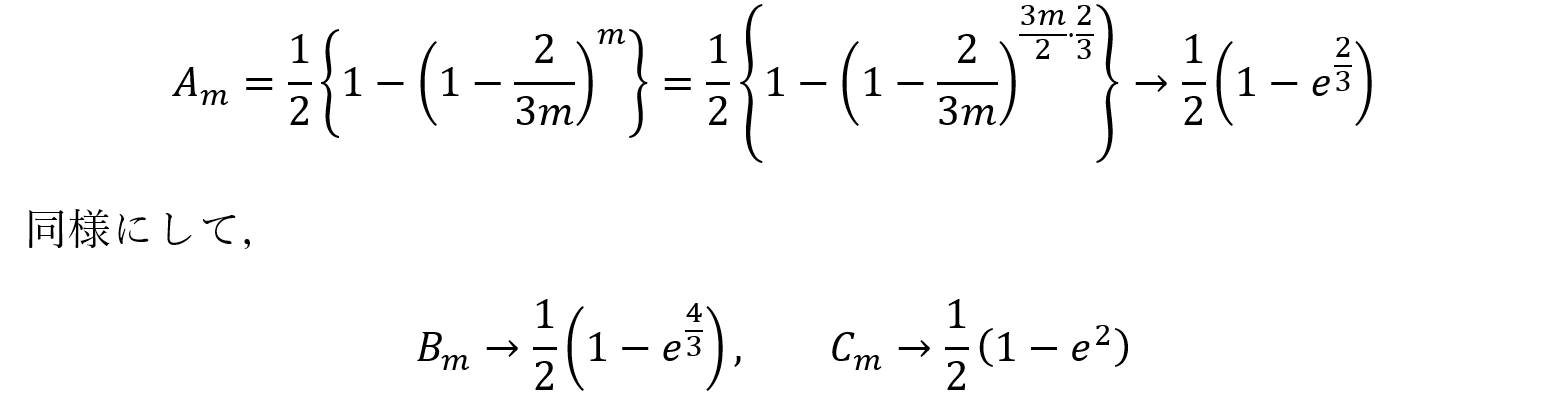
となります。これを②に代入し,
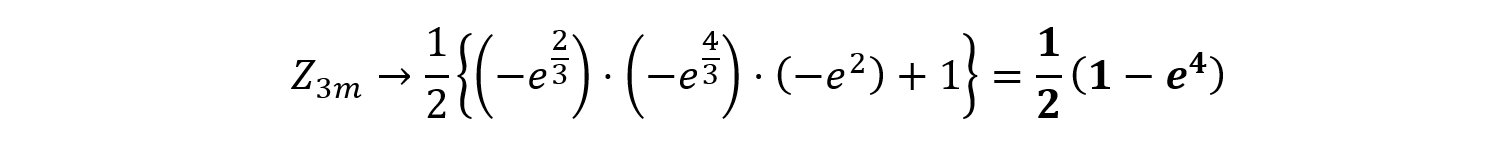
(さらなる検討)
なお,例えば(1)は,漸化式を用いずに直接計算することができます。
n以下の最大の奇数をNとすると,表が出る硬貨が「1枚の確率,3枚の確率,5枚の確率,……,N枚の確率」をすべて足せばよいから,
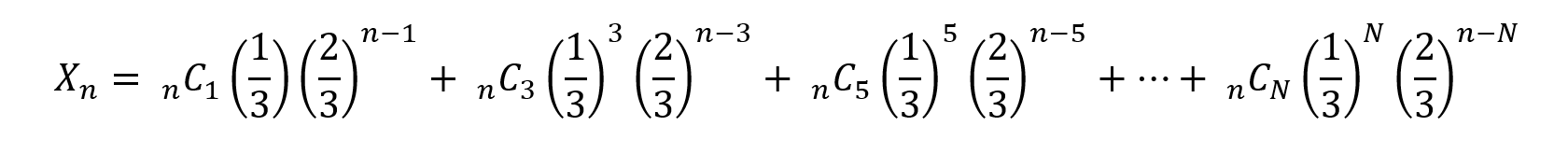
ここで,二項定理より,次の2つの式が得られます。

二項定理によるこの一連の計算は,次のようにまとめることができます。すなわち,
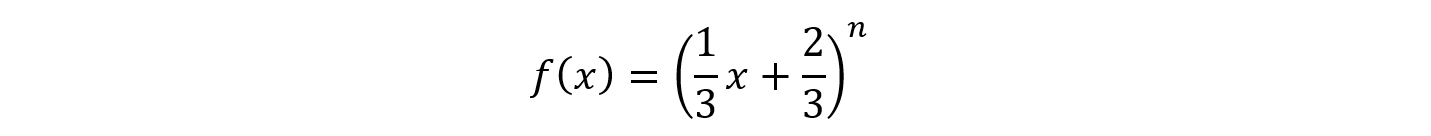
とおくと,Xnは,これを展開した式のうち,xの指数が奇数である項の係数の総和だから,
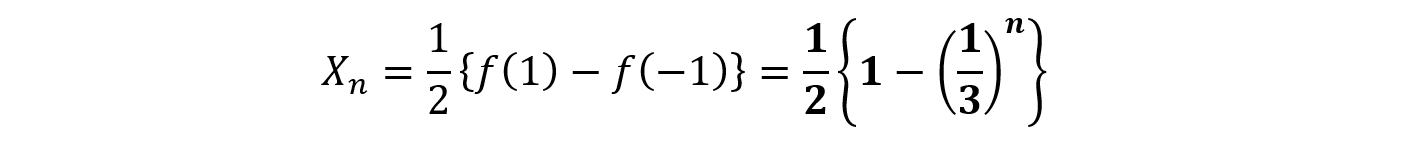
この考え方のヒントは,次の問題にあります。
(問) 360(=23×32×5)の約数の総和は?
(解)
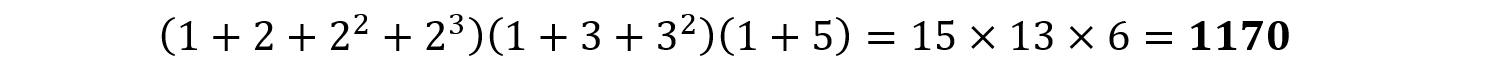
これは,左辺のカッコを分配法則により展開すると,すべての約数の和が現れることによります。これを本問に応用させると,上のような考え方になります。展開で利用する分配法則にはこのような特性があるわけです。
もちろん,(3)についても同様に,
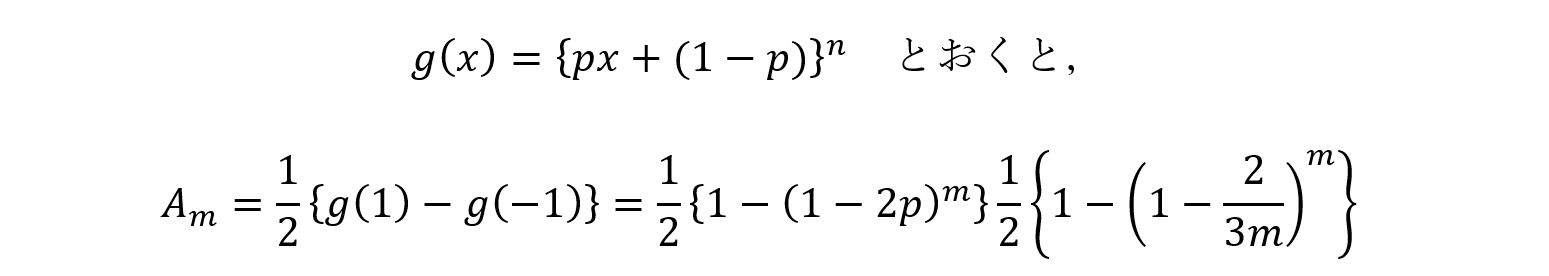
となり,先の結果と同一の結果を得ることができます。
Bm, Cmについても全く同様なので,これ以降は省略します。
さらに,(3)について,別のアプローチも可能です。
簡単のため,まずm=1(硬貨が3枚)の場合を考えますが,後々の応用のために,確率そのものはmを残したままで記載しておきます。
3枚の硬貨について,[表が出る確率,裏が出る確率]はそれぞれ,
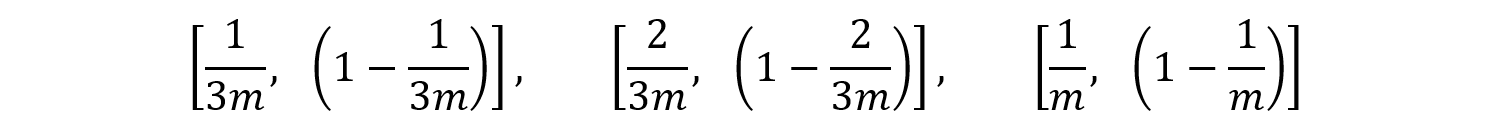
です。表が出る硬貨が奇数枚であるのは,1枚の場合と3枚すべての場合の2通りがあり,
・1枚の場合は,
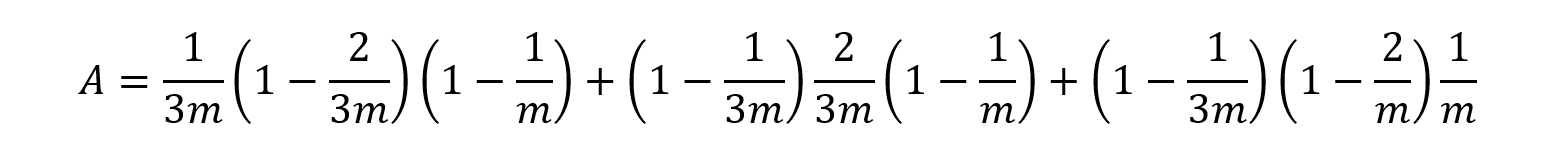
・3枚の場合は,
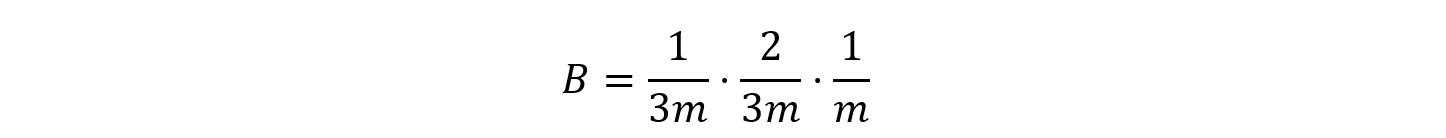
となります。特にAの式が分かりやすいですが, 1枚の硬貨の表が出る確率と,残り2枚の硬貨の裏が出る確率とが,総当たりで現れていることが確認できます。
そこで,上に示した約数の総和の問題をヒントに,次の式を考えてみましょう。
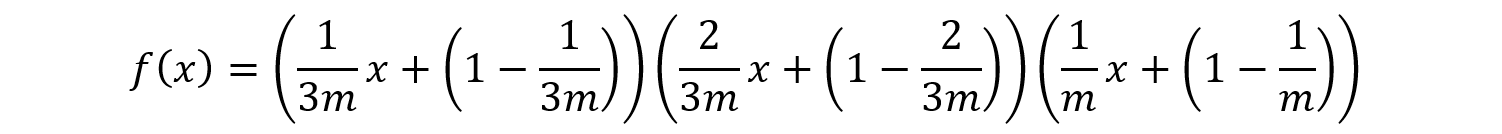
これを展開すると,xの係数がAに,x3の係数がBになっていることが確認できます。
mが一般の場合には,
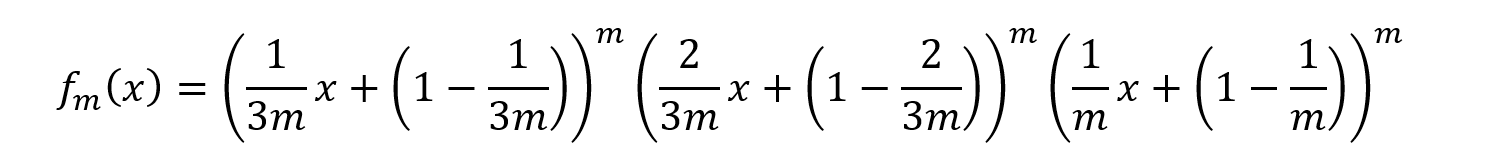
とおくと,この展開式のxiの項の係数が,表が出る硬貨がi枚である確率が現れます!
このことから,Z3mは,iが奇数である項の総和を求めればよく(求め方は,先の二項定理により導出した③と④の2式を辺々引いたのと同じ考え方です),
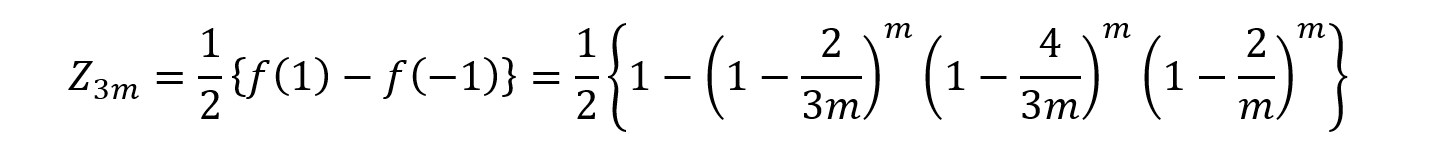
となり,先と同じ結果を得ます。
なお,このような分配法則を利用した工夫により計算量を減らすことができる問題としては,例えば2020年の東京大学・第4問(文理共通)などがあります。興味のある方は,ぜひそちらも解いてみてください。
(まとめ)
東工大の数学は,1問あたりに欠けられる時間が長く(平均35分少々),そのぶん記述量が多くなる傾向にあります。中途半端な知識では手が出ない問題も多く,「深い理解」と「馬力(計算力、記述力)」がともに要求されます。
「深い理解」のためには,定理や公式を自力で導出できることはもちろん,ある問題に対して,様々なアプローチができないかどうか,いろいろ実験してみるのが効果的だと思います。一つの問題に対して一つの解法を覚えたとしても,仮定や数値が変更された場合にそれが最善の解き方ではなくなってしまうかもしれませんし,解けなくなってしまうこともあります。したがって,このときかたはどうだろう,というアイディアが浮かんだら,それが参考書の解答の方針とは異なっても試してみましょう。
つぎに,「馬力」として挙げた「計算力」の土台となるのは「展開」と「因数分解」のスキルです。意外に思われるかもしれませんが,展開や因数分解では,「これらの項をまとまりとしてみるとうまくいきそうだ」とか,「この文字について降べきの順に整理しよう」とか,式そのものに対する観察が求められます。この「恣意的にまとまりを作る」という考え方は,実は他の分野でも生きてきます。さらに,展開や因数分解を暗算で行ってみることも,処理スピードのアップに効果的です。
同時に,解答を「要点を押さえてコンパクトに」記述する訓練も、意識して積んでいきましょう。
これらを踏まえ,ぜひスキルを磨いていってください。
それでは今回はこの辺で!
少人数制 大学受験専門
学習塾Dear Hopeへのお問い合わせ、体験授業のお申込みはこちらからお願いします。
