2020年 京大理系数学 概要と第2問の解説 問題の特殊性に注目しよう
こんにちは、品川区 武蔵小山の学習塾Dear Hope 数学担当の伊藤です。
前回に引き続き、2020年の大学入試で出題された数学の問題のうち、印象的だった問題をご紹介したいと思います。
今回は、京都大学の理系数学についてみていきたいと思います。
今年の出題のセットは、以下の6問でした。
《第1問》 三次方程式の解が複素数平面上で正三角形をなす条件を考察する問題。
《第2問》 二次方程式の解を題材にした二段階の数学的帰納法による証明と数列の極限を求める問題。
《第3問》 球面上に存在する4点が内積を用いて記述された特定の条件を満たすときの各点の位置を考察する問題。(文理共通)
《第4問》 整数m,nを用いて定義された3次式を素因数分解したときの「3」の指数の最大値を求める整数問題。
《第5問》 数独(いわゆるナンプレ)を題材にした場合の数の問題。(文理共通)
《第6問》 回転体の体積を求める問題。
以上の6問です。
独断と偏見で難易度を付けると、難しい順に、4>3>2>5>6>1でしょうか。全体的には、昨年よりも難易度は上昇しました。
京大と言えば図形と整数ですが、やはり第1問、第3問に図形、第4問に整数を出題してきました。
さらに、京大は「読解力」を試す問題を出題する傾向にあります。今年は、第4問の整数問題でした。題意を把握できさえすれば、着想は難しくないと感じましたが、処理に手数を要するため時間内で完答するにはかなりの実力が必要かと思います。
全体を通じ、方針さえ立てられれば、あとは比較的単調な処理(と言っても技術的には高度です)が続く問題が多く、東大と比べるとややドライな印象です。
今年のセットは、印象的な問題が多くありましたが、まず今回は第2問についてみていきたいと思います。実はこのタイプの問題は、これまでにも複数、出題実績があるのです。
以下、第2問の問題文を引用します。

さて、本問は、(2)が勝負の分かれ目でした。(2)を解き切るためには、「βの絶対値が1より小さい」こと、さらに「βが-αの逆数(β=-1/α)である」ことに気づく必要があります。
これらの事項を利用することにより、(2)を簡単な極限の計算に持ち込むことができます。
本問がなぜ印象的なのかというと、
「また出題されたか!」
ということです。
類似問題を以下に引用します。
まず、2019年の早稲田大学(商学部)で出題された問題です。

次は、2003年の東京大学(理系)で出題された問題です。

これらの問題に共通していることは、「絶対値が1より小さい数を2乗、3乗、4乗、…と乗じていくと0に近づいていく」という性質がカギになっている、ということです。
本問は、まず(1)の結果と、β=-1/αという関係から、

と変形することができます。(1)で証明させられた「偶数」という事実が役立ちました。
次に、
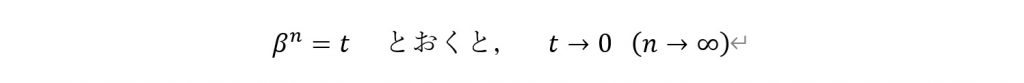
となります。すると、以下のようにして答えにたどり着くことができます。

本問は、「β」を調べずに単に記号のまま扱っていると解けません。βにも人格(?)があるので、「βはβでしょ」と思わず、詳しく調べてあげる必要があるわけです(笑)。丁寧な観察により問題の具体的状況を的確に把握することが求められます。
応用的・発展的な問題を処理するには、通り一辺倒な手法ではうまくいかないケースが多くなってきます。その場合は、授業でも常にお話しているように、その問題の特殊性に着目することが不可欠です。今回の問題の特殊性は、まさに、βの絶対値が1より小さく、β=-1/αである、ということになります。
さて、先に紹介した早稲田の問題ですが、この問題がここまでのお話とどのように関係するかお分かりでしょうか。
本問が問うているのは、要するに、「5+2√5の100乗」の整数部分の下2桁(1の位と10の位)です。
実は本問は、問題文に登場している「5+2√5」に加えて、「5-2√5(=β<1)」という数を解答者が自ら持ち出してくる必要があります。そして、「5-2√5」の絶対値が1より小さいことに着目して解いていきます。ノーヒントで出題されていますので、かなり難易度の高い問題と言えるでしょう。
すなわち、α=5+2√5,β=5-2√5とおくと,求めるものは「αの100乗の整数部分の下2桁」です。
以下、αの100乗とβの100乗を2項定理で展開してみましょう。

となります。αの100乗だけを二項定理で展開しても、「ルート」が解消せず、下2桁を求めることは困難です。このため、αの「片割れ」のβを持ち出して、二人の協力体制(?)のもとで処理を進めていきます。
さて、上式の右辺を100で割った余り(下2桁)を求めます。
まず,5の100乗を100で割った余りは25です。これは、5のべき乗の下2桁が常に25ですから、少し検討すると見えてきます。
次に、5の100乗よりも後ろの部分は、すべての項が4×25を因数に持つため100で割り切れます。
したがって,

つまり「αの100乗+βの100乗」を100で割った余りは50であることが分かります。
ここで、βの絶対値が1より小さいことから、「βの100乗」は当然1よりも小さい正数です。このことを踏まえると、「αの100乗の整数部分の下2桁」は、49であることが分かります。
これが、すなわち求める数です。
難しいですね。なぜこれが文系で出題されているのかは謎です(笑)
もっとも、早稲田の商学部や慶応の商・経済学部系は、数学の難易度が文系学部において日本トップですから、しかたありません。
なお、3番目に紹介した東大の問題も、同じ発想で処理を進めていきます。先に見た早稲田の問題よりは取り組みやすい言えるでしょう。
ここでお話した発想は、公式や解法パターンを暗記する勉強だけでは、出てきにくいと思います。したがって、難関大を目指す皆さんは、日ごろから、この問題ならではの状況設定は何であるか、ということを意識し、多角的に粘り強く考える訓練を積んでいくことが大切だと思います。
それでは今日はこのへんで。
今後も引き続き、良問を紹介していきたいと思います。
◆◆ 無料動画のご案内◆◆
~数学偏差値70を超えていくための「高校数学テクニック集」~
本記事を執筆した講師による、当塾オリジナルの映像教材です。Youtubeにアップしています。こちらのページよりご覧ください。
品川区武蔵小山 学習塾Dear Hopeへのお問い合わせはこちらからお願いします。
