2024年度 東大入試(文系数学)レビュー:数学的な”感覚”が差を生むセット
こんにちは。品川区にある大学受験のための少人数制の学習塾「Dear Hope」副塾長の伊藤です。
今回は、先日実施された国立大の入試から、東京大学(文系)の数学について所感など記していきたいと思います。
解いてみて率直に、「理系より面白いな」と感じました。どちらかというと事務的手続きが多い理系の問題に比較して、数学的な”感覚”が要求されるというか、式の意味を踏まえて議論を展開しなければ行き詰まってしまうような問題が目立ちました。
(数学的な”感覚”は訓練で養えますので安心してください。)
そういう意味で、昨年より難易度が上がりましたので、出来、不出来の差が明確に表れたのではないかと推測します。
では早速、具体的に見ていきたいと思います。今年も4題のセットで、テーマは次の通りです。
(第1問) 座標平面で放物線と単位円が2本の共通接線をもつ条件を考察させる問題と(前半)、その放物線とx軸とで囲まれた図形の面積の最小値を示す問題(後半)。
前半はよくある図形と方程式の問題でした。後半が勝負の問題です。式の中に変数(s)の逆数を含む(したがって、2次関数や3次関数ではない)関数の最小値を検討させる問題でした。
相加平均・相乗平均なのかな、と思った受験生もいたかもしれませんが、そうではありません。詳細は後述します。
(ちなみに,「相加・相乗」は昨年すでに出題済みです。)
(第2問) 「5m+4m>1019」となる最小の自然数mを求める問題。
(1)は「5m>1019」を満たす最小の自然数mを求めよ、という問題で、これと同じmの値がそのまま答えになることを論証する問題でした。したがって、このことを最初の段階で想像できたか否かが、明暗を分けたと思います。
(第3問) 所定の条件にしたがって規定された二つの三角形の頂点の座標や、面積の大小を検討する問題。
図形と方程式の分野に属する問題です。直線とx軸またはy軸のなす角度θを用いて直線の傾きを求めるような作業を的確に行えるよう訓練を積んだ受験生にとっては、やりやすい問題だったと思われます。
(第4問) 点Oを中心とする正n角形のn個の頂点から4点を選んで四角形を作ったとき、その四角形の内部に点Oが含まれる確率を求める問題。
本問は、このようなタイプの問題を解いたことが無い受験生にとってはお手上げだったのではないでしょうか。いくつかの処理方法が考えられますが、例えば、最も長い辺のとり方に注目して求めるなど、技術が必要です。
独断と偏見による難易度としては、
(易)3≦1≦2<4(難)
だと思います。第1問、第2問、第3問のうち2問程度をしっかりと解けたかが、合否を分けたと思われます。
以下、問題を引用しつつ詳しく見ていきたいと思います。
(第1問)
問題.jpg)
(出典:2024年度 東京大学入試問題 数学(文系)第1問)
1)は放物線Cが点PおよびQを通過すること、さらに、原点と接点とを結ぶ直線が共通接線と直交する条件を考えることにより求めることができます。
(2)は、いわゆる「1/6公式」などを用いて計算すればOKです。この結果、面積Aは次のようになります。
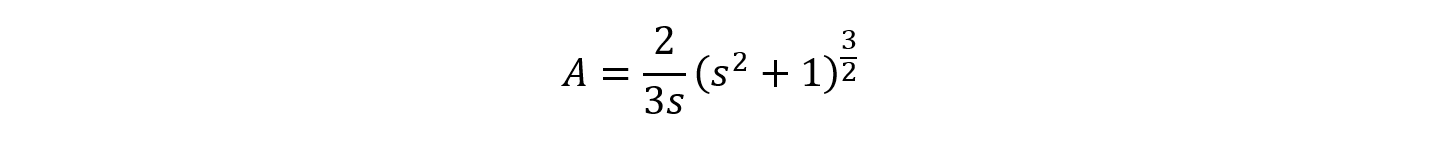
さて、(3)では、この式の最小値が√3であることを証明します。 ポイントは、「最小値を求めよ」という問いになっているのではなく、「Aが√3以上であることを示せ」という問いになっていることです。いま、明らかにsは正ですから、Aは正です。ゆえに「A2-3≧0」を示していきます。

これが0以上になることを示せばOKです。ところで、カッコの前についている「1/9t」は正です。したがって、「カッコの中身が0以上」を示せばOKです。 このことに気づけたかどうかが、ポイントです。
あるいは,次のように最小値を直接求めることも可能です。

.jpg)
これはいわゆる逆像法(逆手流)と呼ばれる考え方です。逆像法は,直線などの図形の通過領域を求める際に用いられることが多いですが,このように関数の最大値や最小値を求める際にも活用することができます。
(第2問)

(出典:2024年度 東京大学入試問題 数学(文系)第2問)
本問は常用対数に関する問題です。計算手続き自体は平易ですが、(2)は「527と比較して427はとても小さい数だから、(1)で求めたnの値か、あるいはその値より1少ない数以外に答えは無いだろう」という感覚が大切だと思います。
さて、(1)の答えはn=28ですが、これは典型問題なので詳細は省略します。
この結果から、(2)の答えは「27か28」と推測されます。そこで、「527+427」がどの程度の値かを検討していきましょう。この値が1019よりも大きければ27が答えだし、それより小さければ28が答えになるわけです。

なお、N+M=527+427を次のように評価することも可能です。
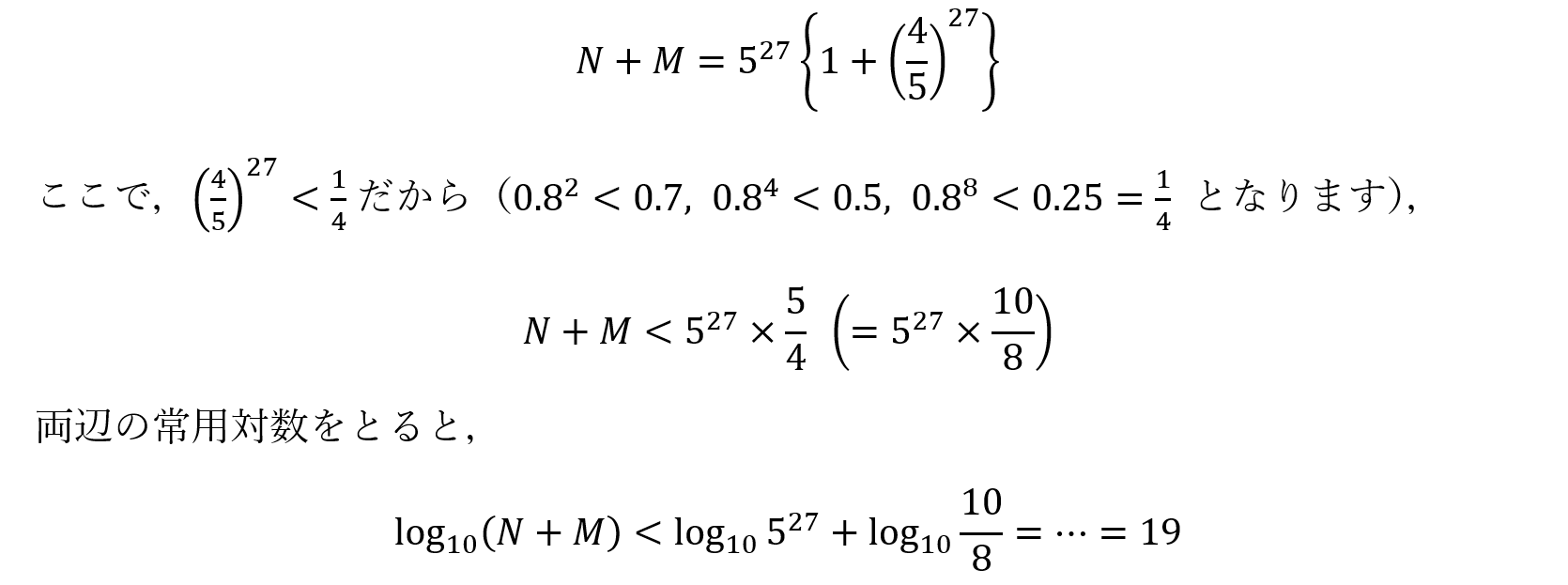
ゆえに、N+M<1019 であるから、n=27 は問題に適していないことが分かりました。
最後に、第4問を見ていきます。
(第4問)

(出典:2024年度 東京大学入試問題 数学(文系)第4問)
まず、下の図のように、n個の頂点を反時計回りにA0~An-1と定めましょう。

本問に近い問題として、正n角形の頂点から3つを選んで三角形を作るとき、その三角形が鈍角三角形になる確率を求めよ、という問題があります。この問題を解く際には、最長辺に注目すると効率的であることが知られています。
そこで本問でも、四角形の「最長辺」に注目し、余事象(四角形が点Oを内部に含まない事象)を考えます。

このように答えを求めることができました。
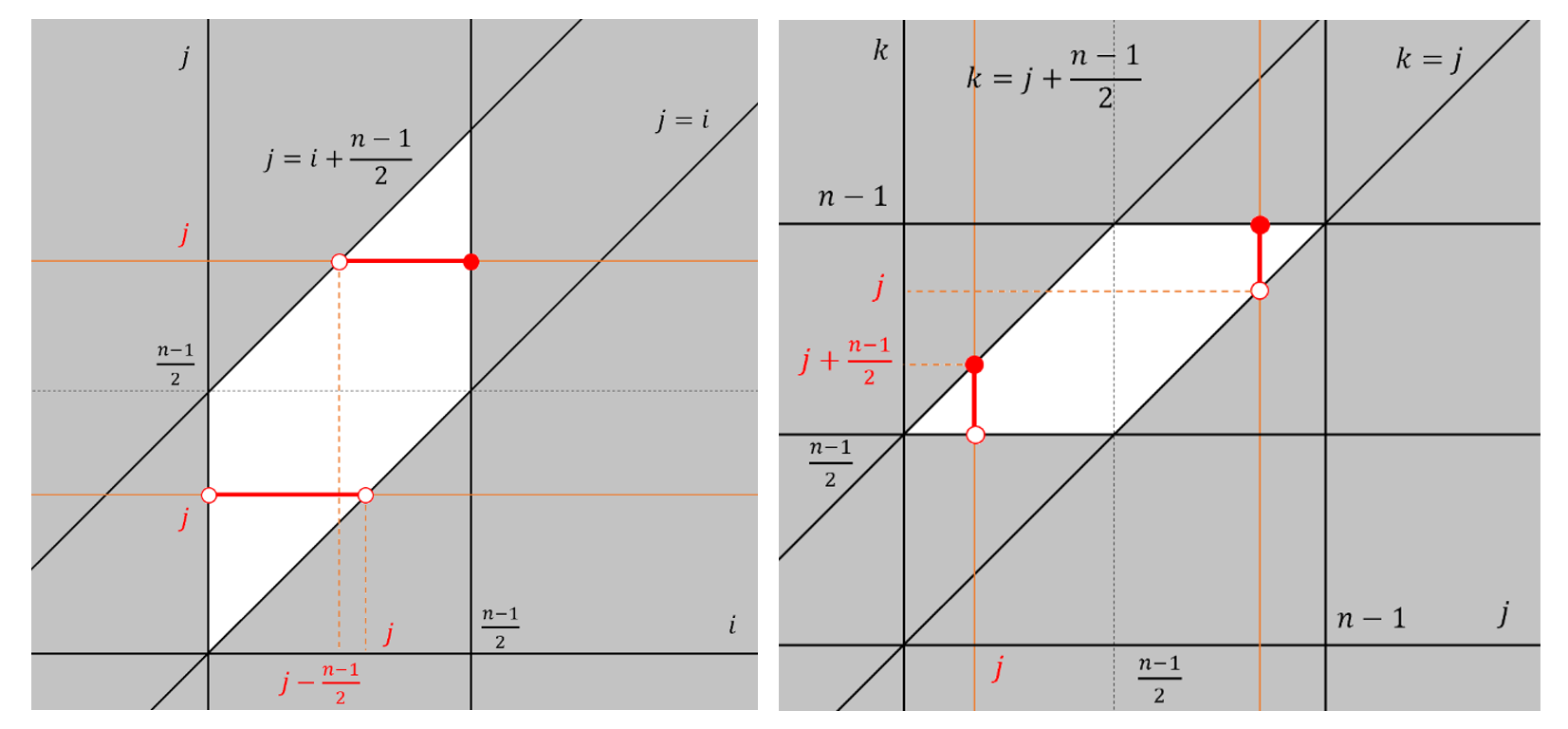
研究のため、式を機械的に処理していく方法でも試しに解いてみます。先ほどと同様に、四角形の1つの頂点をA0に固定し、残り3つの頂点を反時計回りの順にAi、Aj、Akと定めます(ただし、1≦ⅰ<j<k≦n-1)。
点Oが四角形の内部に含まれるためには,四角形の各辺を反時計回りに辿るとき、常に点Oが辺の左側にあればよいから、ⅰ、j、k の間に
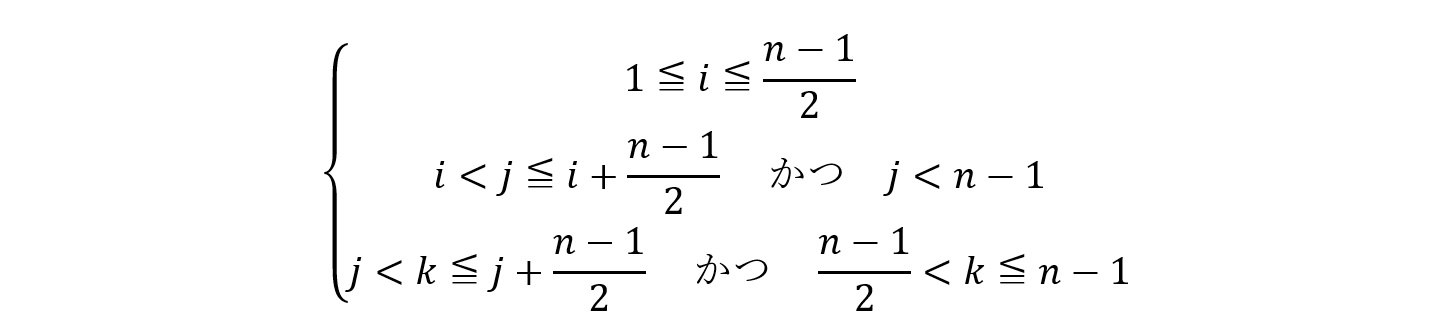
が同時に成立する条件を考えればよいわけです。なお,たとえば
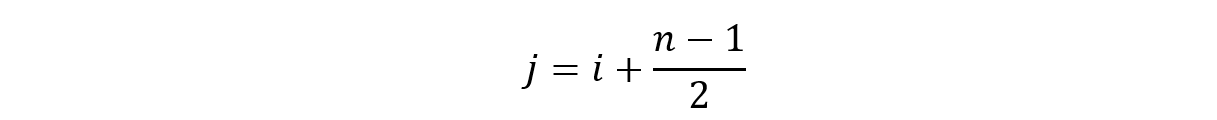
のときというのは、点Oに関し点 Ai のちょうど反対側の地点に最も近い2つの頂点のうち、番号が小さい方の頂点が Ajということです。これよりもj が大きくなると、点Oが辺の右側に来てしまいます。
さて、上の連立不等式を満たす整数の組(ⅰ,j,k)の数をan とすると、題意を満たす四角形の個数は
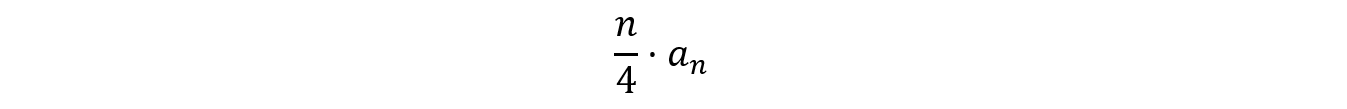
です。なぜなら、A0 に固定していた頂点を A1、A2、⋯、An-1 に順次変化させたときも全く同様であり、さらに、このように考えると1つの四角形を4回ずつカウントするからです。
では、以下にan を求めていきます。

以上から、

このように、ⅰ,j,kが満たすべき条件式を立てることができれば、あとは格子点の問題として機械的に処理することができました。この手法を本番で採用するかは別として、特に理系の皆さんはこのような処理方法にも慣れておくと役立つ場面があるはずです。
(まとめ)
以上のように、今年の東大のセットは、暗記で何とかしようとか、テクニックを覚えよう、というスタンスで学習に取り組んできた方には厳しい問題だったと思いますが、数学の考え方を深く丁寧に学習していた受験生にとっては十分に合格ラインを超えることができたセットだったと思います。
毎年のように訴えているところではありますが、東大を目指す皆さんは、ぜひ根本的な理解を大切にして学習に取り組まれることをお勧めします。
理系のブログにも書いた通り、自分がしっかりと理解できているかどうかは、定理や解法を黒板の前に立って他人に分かりやすく説明することができるか、をイメージして自問自答すれば明らかです。このような根本的な理解が、難関大で求められる「応用力」を養ってくれます。
それでは今回はこのへんで!
少人数制 大学受験専門
学習塾Dear Hopeへのお問い合わせ、体験授業のお申込みはこちらからお願いします。
